A biconvex thin lens is prepared from glass , the two bounding surfaces having equal radii of 25 cm each. One of the surfaces is silvered from outside to make it reflecting. Whee should an object be placed before this lens so that the image is formed on the object itself?

The correct Answer is:
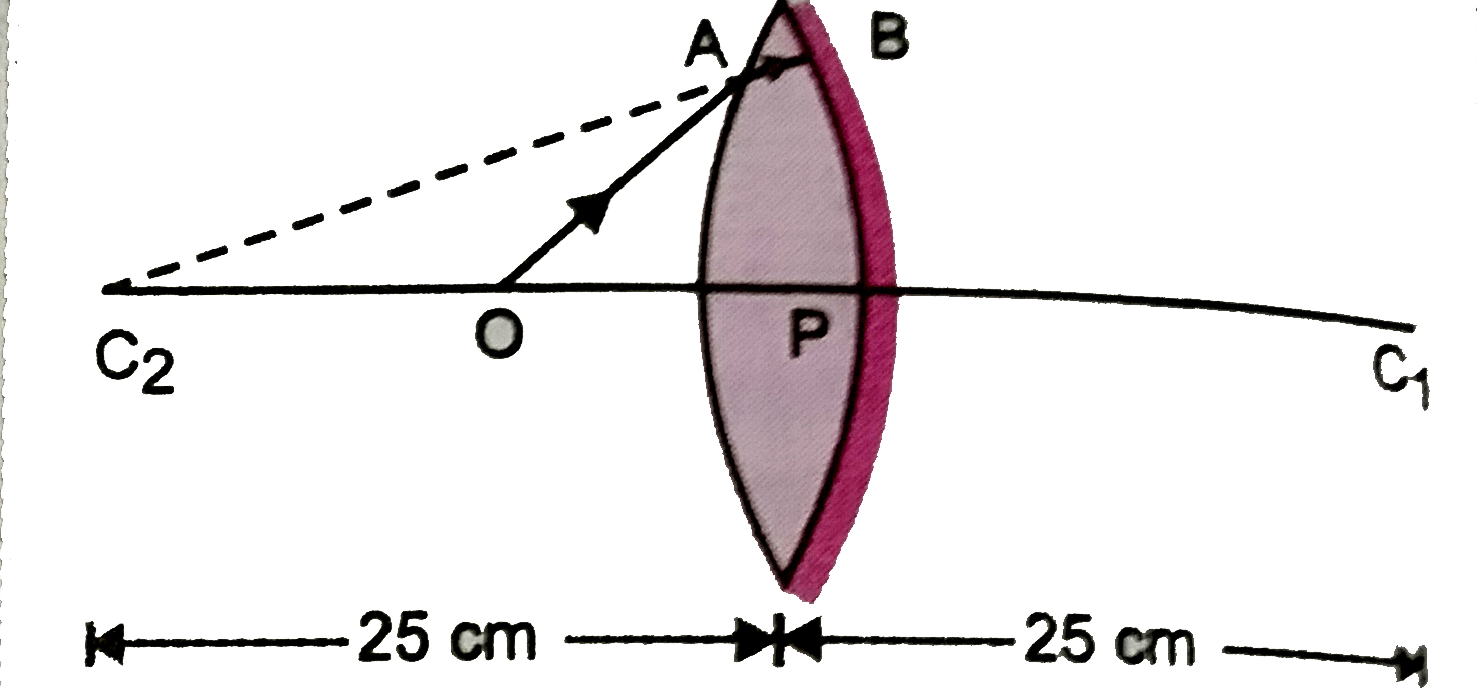
In Fig., let the object be placed at The ray is refracted along at first surface and hits the silvered surface. To get the final image at should fall normally on silvered surface. Therefore, should appear to come from centre of curvature of second surface.
Thus ,
.
Refraction from rarer to denser medium
Solve to get
Thus the object should be placed at a distance of to the left of the lens.
 .
.
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(c)
27 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(d)
35 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Long Answer (a)
5 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
A biconvex thin lens is prepared from glass of refractive index 3/2. The two bounding surfaces have equal radii of 25cm each. One of the surfaces is silvered from outside to make it reflecting. Where should an object be placed before this lens so that the image coincides with the object.
View SolutionA diverging lens of focal length 12 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself ?
View Solution
Knowledge Check
A biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
Aconverging mirrorBdiverging mirrorCconcave mirror of focal length 12.5 cmDconvex mirror of focal length 12.5 cmFocal length of an equiconvex lens is 20 cm. The refractive index of material of the lens is 1.5. Now one of the curved surface is silvered. At what distance from the lens an object is to be placed, so that image coincides with the object ?
A10 cmB20 cmC30 cmD40 cm
A convex lens of focal length 20cm is placed 10cm in front of a convex mirror or radius of curvature 15cm. Where should a point object be placed in front of the lens so that it images on to itself?
View SolutionA biconvex thick lens is constructed with glass (mu = 1.50). Each of the surfaces has a radius of 10 cm and the thickness at the middle is 5 cm. Locate the image of an object placed far away from the lens.
View SolutionA biconvex lens is made of glass with refractive index 1.5 and has radii of curvature 20 cm and 30 cm. If the 20 cm surface is silvered, what is the effective focal length of the mirror formed?

View SolutionA glass slab of thickness 2cm and refractive index 2 is placed in contact with a biconvex lens of focal length 20cm. The refractive index of the material of the lens 1.5 . The far side of the lens is silvered. Where should an object be placed in front of the slab so that it images on to itself?
View SolutionA biconvex lens is made of glass with μ=1.52. Each surface has a radius of curvature equal to 30cm. An object of height 3cm is placed 14cm from the lens. Find the focal length of the lens and the position and size of image.
View Solution
As shown in figure. L is half part of an equiconvex lens (μ=1.5) whose surface have radius of curvature R=40cm and its right surface in silvered. Normal to principal axis, a plane mirror M is placed on the right of lens. A small object O is placed on left of the lens such that there is no parallax between final images formed by the lens and mirror. If transverse length of final image formed by the lens is twice that of image formed by the mirror. Calculate distance a between lens and object and distance b.
View Solution
