A binary star system consists of two stars A and B which have time period $T_{A} and T_{B}, r a d i u s R_{B} a$ and mass $M_{a} and M_{B} .$ Then

A

$if$ T_Agt T_B then R_A gt R_B

B

$if T_{A} > T_{B} t h e n M_{A} > M_{B}$

C

${(\frac{T_{A}}{T_{B}})}^{2} = {(\frac{R_{A}}{R_{B}})}^{3}$

D

$T_{A} = T_{B}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:D

To solve the problem regarding the binary star system consisting of two stars A and B, we need to analyze the relationship between their time periods, masses, and radii. Here’s a step-by-step solution:
Step 1: Understanding the System
In a binary star system, two stars orbit around their common center of mass. The gravitational force between the two stars provides the necessary centripetal force for their circular motion.
Step 2: Gravitational Force
The gravitational force $F$ between the two stars can be expressed using Newton's law of gravitation:
$F = \frac{G M_{A} M_{B}}{D^{2}}$
where $G$ is the gravitational constant, $M_{A}$ and $M_{B}$ are the masses of stars A and B, respectively, and $D$ is the distance between the two stars.
Step 3: Centripetal Force
For a star to move in a circular path, the required centripetal force $F_{c}$ is given by:
$F_{c} = m ω^{2} r$
where $m$ is the mass of the star, $ω$ is the angular velocity, and $r$ is the radius of the circular path.
Step 4: Equating Forces
Since the gravitational force provides the centripetal force for both stars, we can set the gravitational force equal to the centripetal force for each star:
$\frac{G M_{A} M_{B}}{D^{2}} = M_{A} ω^{2} R_{A} (for star A)$
$\frac{G M_{A} M_{B}}{D^{2}} = M_{B} ω^{2} R_{B} (for star B)$
Step 5: Relationship Between Angular Velocity and Time Period
The angular velocity $ω$ is related to the time period $T$ by the formula:
$ω = \frac{2 π}{T}$
Thus, we can express the time periods for both stars:
$T_{A} = \frac{2 π}{ω_{A}} and T_{B} = \frac{2 π}{ω_{B}}$
Step 6: Conclusion
Since the angular velocities $ω_{A}$ and $ω_{B}$ are equal for both stars (as they orbit around the center of mass), we conclude that:
$T_{A} = T_{B}$
This means the time periods of both stars are the same.
Final Answer
Thus, the correct option is that the time periods of the two stars are equal:
$T_{A} = T_{B}$

|

Updated on:7/8/2024

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219videos
HEAT AND THERMODYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
A binary star system consists of two stars. One star has twice the mass of the other. The star rotates about their common centre of mass. Which of the following statement is correct?
AStar having the smaller mass has twice angular momentum compared to heavier star.
BBoth stars have same angular momentum about centre of mass.
CBoth stars have same linear speed.
DBoth the stars have same kinetic energy.
Question 2 - Select One
A binary star system consists of two stars of masses $M_{1}$ and $M_{2}$ revolving in circular orbits of radii $R_{1}$ and $R_{2}$ respectively. If their respective time periods are $T_{1}$ and $T_{2}$ , then
A $T_{1} > T_{2}$ if $R_{1} > R_{2}$
B $T_{1} > T_{2}$ if $M_{1} > M_{2}$
C $T_{1} = T_{2}$
D $\frac{T_{1}}{T_{2}} = {(\frac{R_{1}}{R_{2}})}^{3 / 2}$
Question 3 - Select One
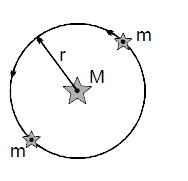
An isolated triple star systerm consists of two identical stars, each of mass $m$ and f fixed star of mass $M$ . They revolve around the central star in the same circular orbit to radius $r$ . The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:
A $\frac{4 π r^{3 / 2}}{\sqrt{G (4 M + m)}}$
B $\frac{2 π r^{3 / 2}}{\sqrt{G M}}$
C $\frac{2 π r^{3 / 2}}{\sqrt{G (M + m)}}$
D $\frac{4 π r^{3 / 2}}{\sqrt{G (M + m)}}$

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-GRAVITATION-JEE Main And Advanced

Home
Ask Doubt
Profile