A binary star system consists of two stars A and B which have time period TAandTB,radiusRBa and mass MaandMB. Then
( if TA>Tb, then RA gt Rg
( if TA gtTb, then MA gt MB
((T(T)2=((R(R□)V
(TA=TB
Step by step video solution for A binary star system consists of two stars A and B which have time period T_A and T_B, radius R_Ba and mass M_a and M_B. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A binary star system consists of two stars A and B which have time periods TA and TB radius RA and RB and masses mA and mB which of the three quantities are same for the stars. Justify.
View SolutionConsider a binary star system consisting of two stars of masses M1 and M2 separated by a distance of 30AU with a period of revolution equal to 30 years. If one of the two stars is 5 times farther from the centre of mass than the other, show that the masses of the two stars are 5 and 25 times that of the sun.
View Solution
Knowledge Check
A binary star system consists of two stars. One star has twice the mass of the other. The star rotates about their common centre of mass. Which of the following statement is correct?
AStar having the smaller mass has twice angular momentum compared to heavier star.BBoth stars have same angular momentum about centre of mass.CBoth stars have same linear speed.DBoth the stars have same kinetic energy.A binary star system consists of two stars of masses M1 and M2 revolving in circular orbits of radii R1 and R2 respectively. If their respective time periods are T1 and T2, then
AT1>T2 if R1>R2BT1>T2 if M1>M2CT1=T2DT1T2=(R1R2)3/2An isolated triple star systerm consists of two identical stars, each of mass m and f fixed star of mass M. They revolve around the central star in the same circular orbit to radius r. The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:
 A4πr3/2√G(4M+m)B2πr3/2√GMC2πr3/2√G(M+m)D4πr3/2√G(M+m)
A4πr3/2√G(4M+m)B2πr3/2√GMC2πr3/2√G(M+m)D4πr3/2√G(M+m)
A certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
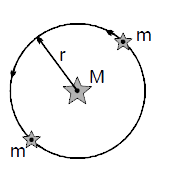
View SolutionA binary star consists of two stars A(mass2.2Ms) and B (mass11Ms) where Ms is the mass of the sun, they are separted by distane d and are rotating about their center of mass, which is stationary. The ratio of the total angular momentum of the binary to the angular momentum of star B about the centre of mass is
View Solution_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:
View Solution_S01_035_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The total machanical energy of the system is
View Solution_S01_034_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The orbital velocity of each star is
View Solution
