Question

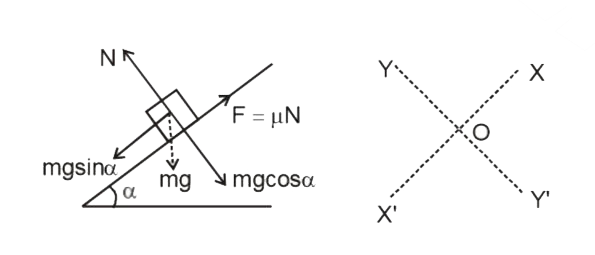
A block is at rest at the top of a rough inclined plane of inclination 30° with the horizontal. What is the coefficient of kinetic friction between the block and the plane, if the . block slides down with an acceleration of $\frac{g}{5}$ ?

Options

A. 0.25
B. 0.275
C. 0.325
D. 0.346

Answer

D

Explanation

To solve the problem, we will analyze the forces acting on the block on the inclined plane and apply Newton's second law.

1. Identify the Forces Acting on the Block:
- The weight of the block (W) acts vertically downward and can be expressed as \( W = mg \), where \( m \) is the mass of the block and \( g \) is the acceleration due to gravity.
- The weight can be resolved into two components:
- Perpendicular to the incline: \( W_{\perp} = mg \cos(30^\circ) \)
- Parallel to the incline: \( W_{\parallel} = mg \sin(30^\circ) \)

2. Calculate the Components of Weight:
- Using the values of sine and cosine for 30°:
- \( \sin(30^\circ) = \frac{1}{2} \)
- \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \)
- Thus, we have:
- \( W_{\parallel} = mg \cdot \frac{1}{2} = \frac{mg}{2} \)
- \( W_{\perp} = mg \cdot \frac{\sqrt{3}}{2} \)

3. Determine the Normal Force (R):
- The normal force \( R \) acting on the block is equal to the perpendicular component of the weight:
\( R = mg \cos(30^\circ) = mg \cdot \frac{\sqrt{3}}{2} \)

4. Apply Newton's Second Law:
- The net force acting along the incline is given by:
\( F_{\text{net}} = W_{\parallel} - F_{\text{friction}} = mg \sin(30^\circ) - \mu_k R \)
- The frictional force can be expressed as \( F_{\text{friction}} = \mu_k R \).
- According to Newton’s second law, the net force is also equal to mass times acceleration:
\( F_{\text{net}} = ma = m \cdot \frac{g}{5} \)

5. Set Up the Equation:
- Equating the two expressions for net force:
\( mg \sin(30^\circ) - \mu_k R = m \cdot \frac{g}{5} \)
- Substituting the values:
\( mg \cdot \frac{1}{2} - \mu_k \left(mg \cdot \frac{\sqrt{3}}{2}\right) = m \cdot \frac{g}{5} \)

6. Cancel Mass (m) and Gravity (g):
- Dividing through by \( mg \) (assuming \( m \neq 0 \) and \( g \neq 0 \)):
\( \frac{1}{2} - \mu_k \cdot \frac{\sqrt{3}}{2} = \frac{1}{5} \)

7. Rearranging the Equation:
- Rearranging gives:
\( \mu_k \cdot \frac{\sqrt{3}}{2} = \frac{1}{2} - \frac{1}{5} \)
- Finding a common denominator (10):
\( \frac{1}{2} = \frac{5}{10}, \quad \frac{1}{5} = \frac{2}{10} \quad \Rightarrow \quad \frac{5}{10} - \frac{2}{10} = \frac{3}{10} \)
- Therefore:
\( \mu_k \cdot \frac{\sqrt{3}}{2} = \frac{3}{10} \)

8. Solving for the Coefficient of Kinetic Friction (\(\mu_k\)):
- Multiply both sides by \( \frac{2}{\sqrt{3}} \):
\( \mu_k = \frac{3}{10} \cdot \frac{2}{\sqrt{3}} = \frac{6}{10\sqrt{3}} = \frac{3}{5\sqrt{3}} \)

Final Answer
The coefficient of kinetic friction (\(\mu_k\)) between the block and the inclined plane is:
\( \mu_k = \frac{3}{5\sqrt{3}} \approx 0.346 \)