A block is tied to one end of a light string of length 1 whose other end is fixed to a rigid support. The block is given a speed of √7gl/2 from the lowermost position. Find the height and speed at which the block leaves the circle. Also find the maximum height to which it rises finally.
As velocity of the block vb√2gl<vb<√5gl.
The block will leave the circle at some point P, where the radius OP makes an angle θ with the upward vertical.
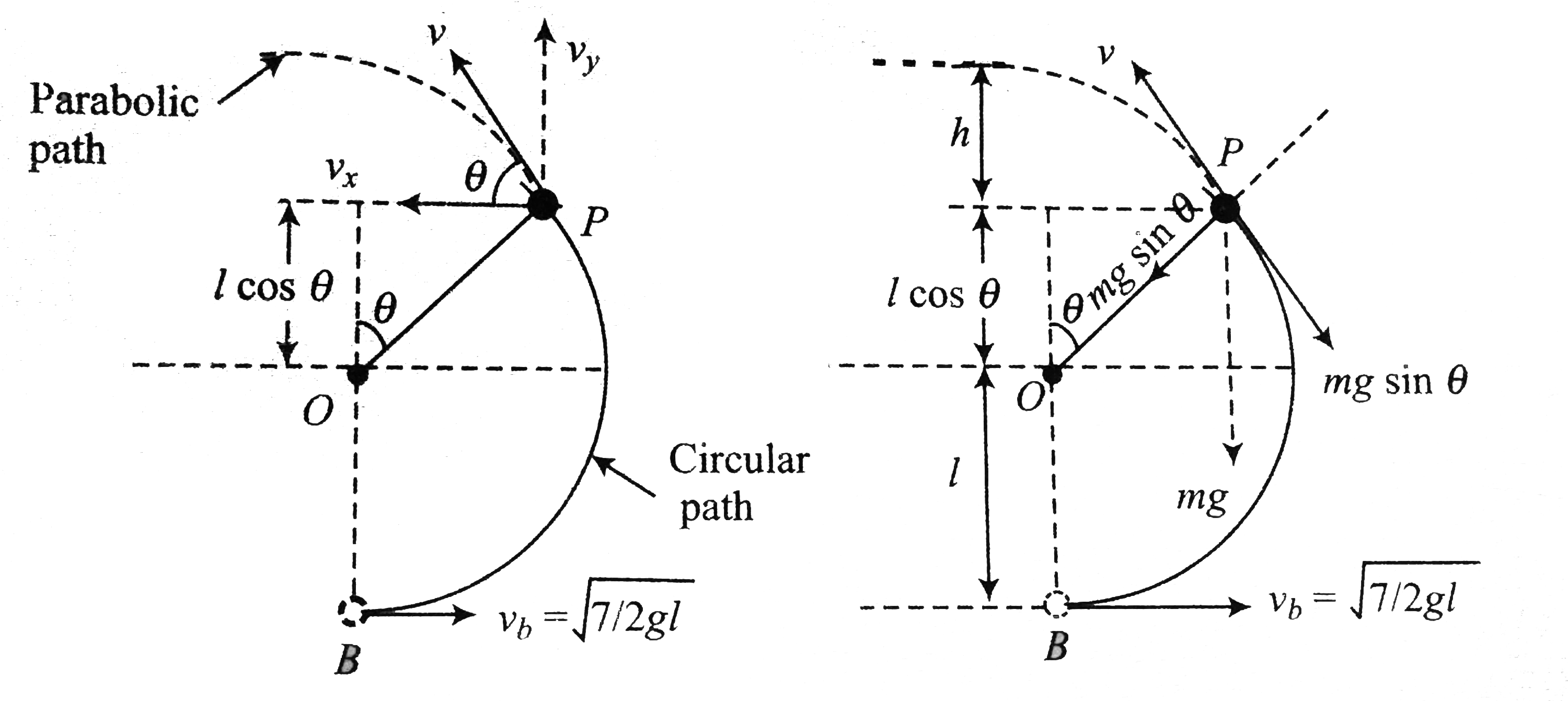
From A to P,
ΔK+ΔU=0 or ΔK=−ΔU
Loss in KE=Gain in GPE
12mv2b−12mv2=mg(l+lcosθ) (i)
From the force diagram: T+mgcos=mv2l
As the block leaves the circle at P, T=0.
mgcosθ=mv2l (ii)
Putting the value of v2 from (ii) in (i) ,
12mv2b−12m(glcosθ)=mgl(1+cosθ)
⇒12m(72gl)=mgl2(2+3cosθ)
⇒cosθ=12⇒θ=60∘
Hence, the block leaves the circle and string slack at a height h=l+lcos60∘=1.5l from the bottom. The velocity at that moment v is v=√lgcosθ=√lg2
After the string becomes slack, the block moves as a projectile in parabolic path. Now, further height attained
=v2sin2θ2g=lg4g(34)=(316)l
Thus, total height attained from the bottom is
32l+316l=2716l
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
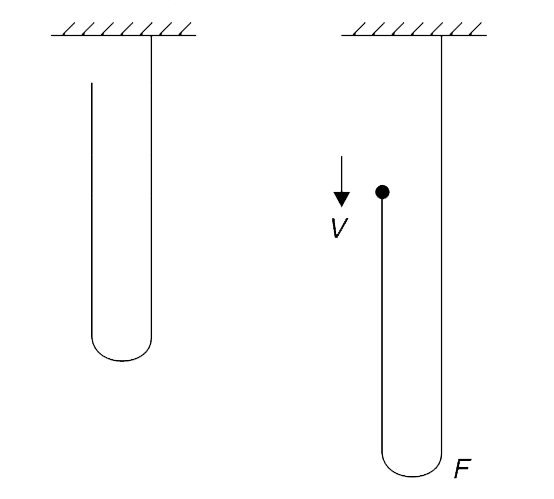
View SolutionOne end of a rope is fixed at a point on the ceiling the other end is held close to the first end so that the rope is folded. The second end is released from this position. Find the speed at which the fold at F is descending at the instant the free end of the rope is going down at speed V.
View Solution
Knowledge Check
A small block of mass m is attached to free end of a spring of force cosntant k , whose other end is fixed to a rigid support . The block is lying on a frictionless horizontal plane and it starts movi0ng away from fixed end of the spring a\t t= 0 with intial velocity u When the speed of the block is 0.6μ it collides with a fixed heavy mass elastically. After the collision with a fixed heavy mass elastically . Aftere the collision the time at which the block passes through its equilibrium position for the first time is close to
Aπ√mKB1.86√mKC2√mKD2π√mKA stone is tied to one end of a light inexensible string of length l and made to roate on a vertical circle keeping other end of the spring at the centre. If speed of stone at the highest point is v(v>√gl) then its speed at the lowest point is
A√4glB√v2+2glC√v2+glD√v2+4glA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these
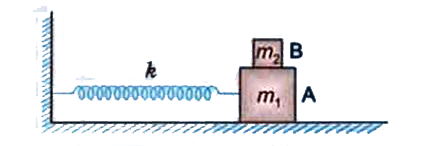
A block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA 2 kg block A is attached to one end of a light string that passes over an an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of 5m/s2 with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the steing. [g=10m/s2]

View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View Solution
