A block mass m=2kg is moving with velocityv0 towards a mass less unstretched spring of the force constant k=10N/m. Coefficient of friction between the block and the ground is μ=0.2. Find the maximum value of v0 so that after pressing the spring the block does not return back but stops there permanently.

√12m/s
√4.2m/s
√10m/s
√6.4m/s
The correct Answer is:D
Step by step video & image solution for A block mass m = 2 kg is moving with velocityv_(0) towards a mass less unstretched spring of the force constant k = 10 N//m. Coefficient of friction between the block and the ground is mu = 0.2. Find the maximum value of v_(0) so that after pressing the spring the block does not return back but stops there permanently. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
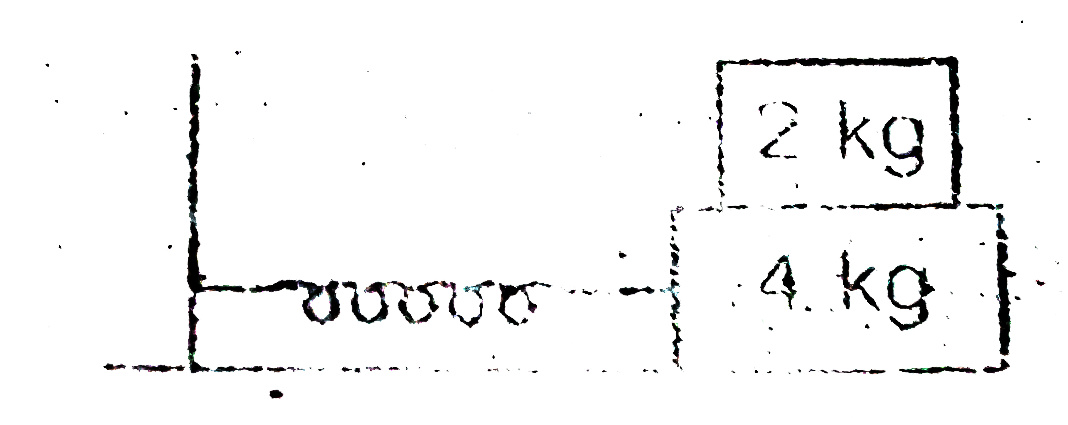
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

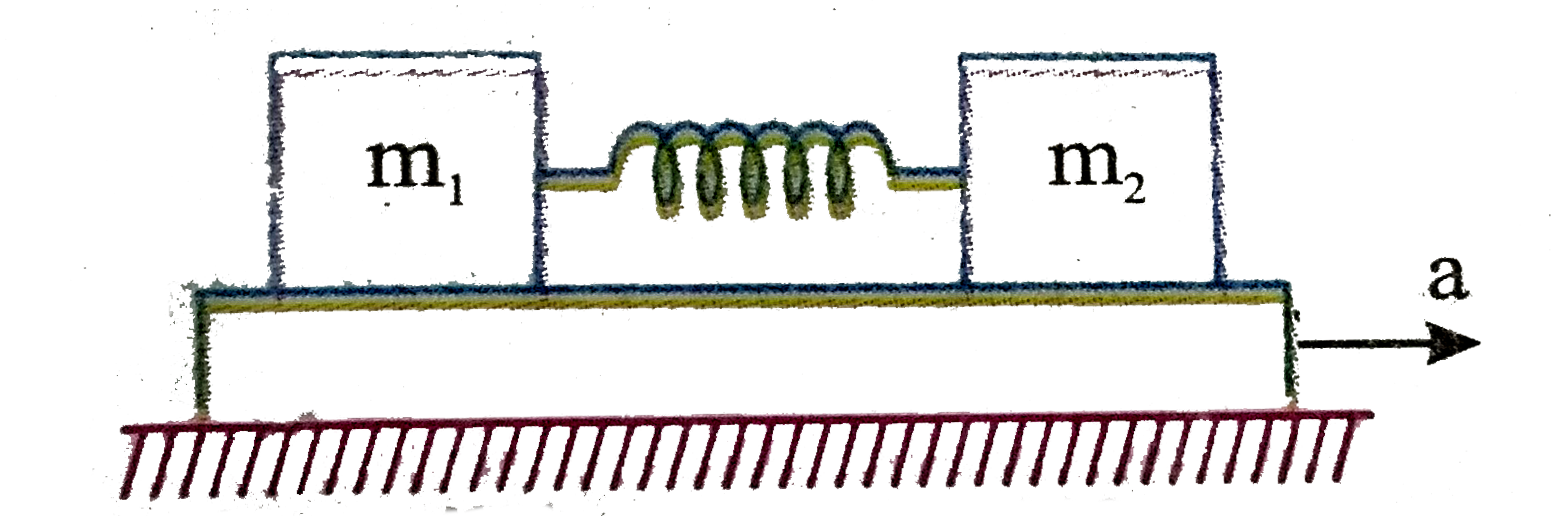
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
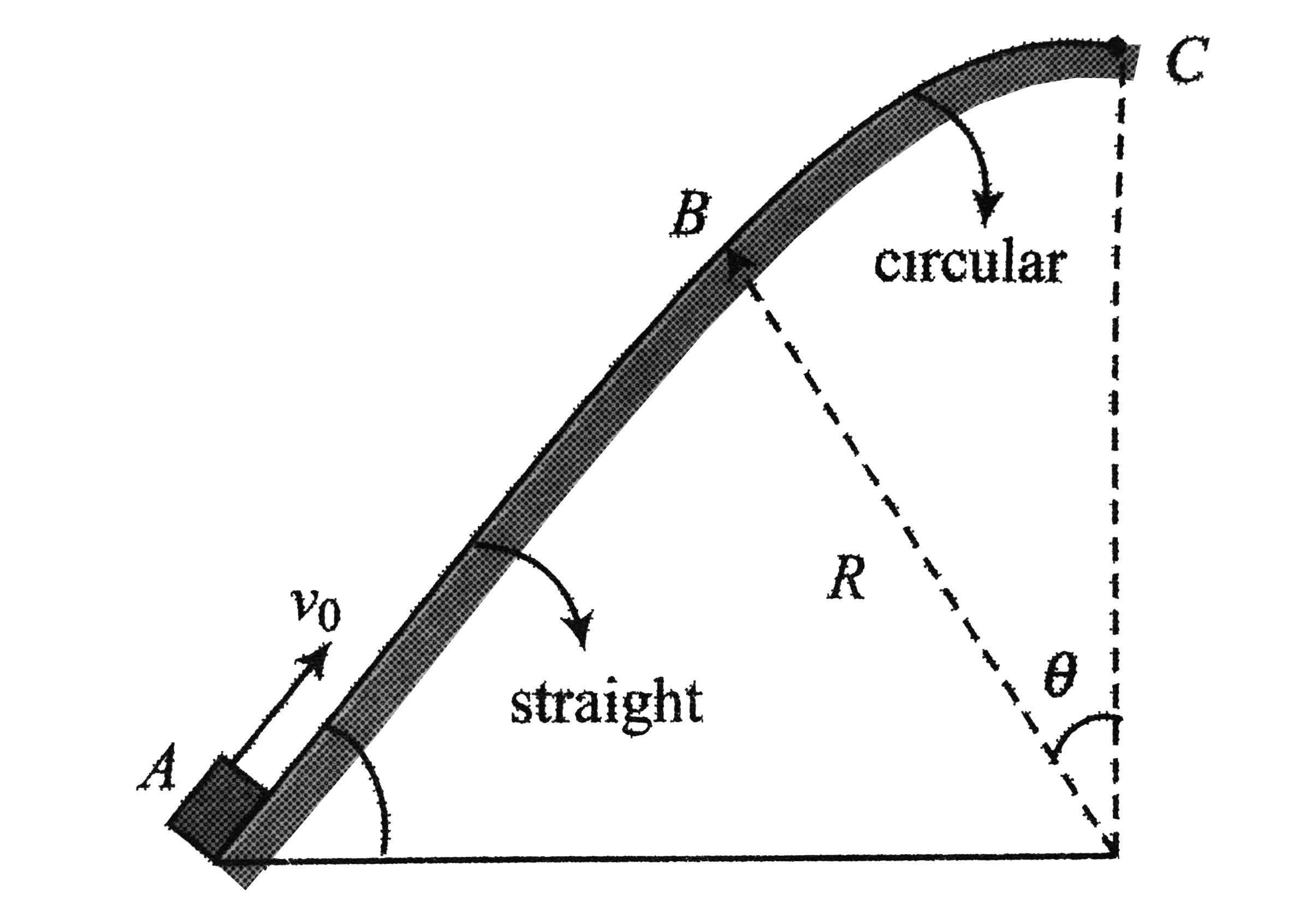
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
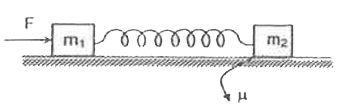
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View SolutionA block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
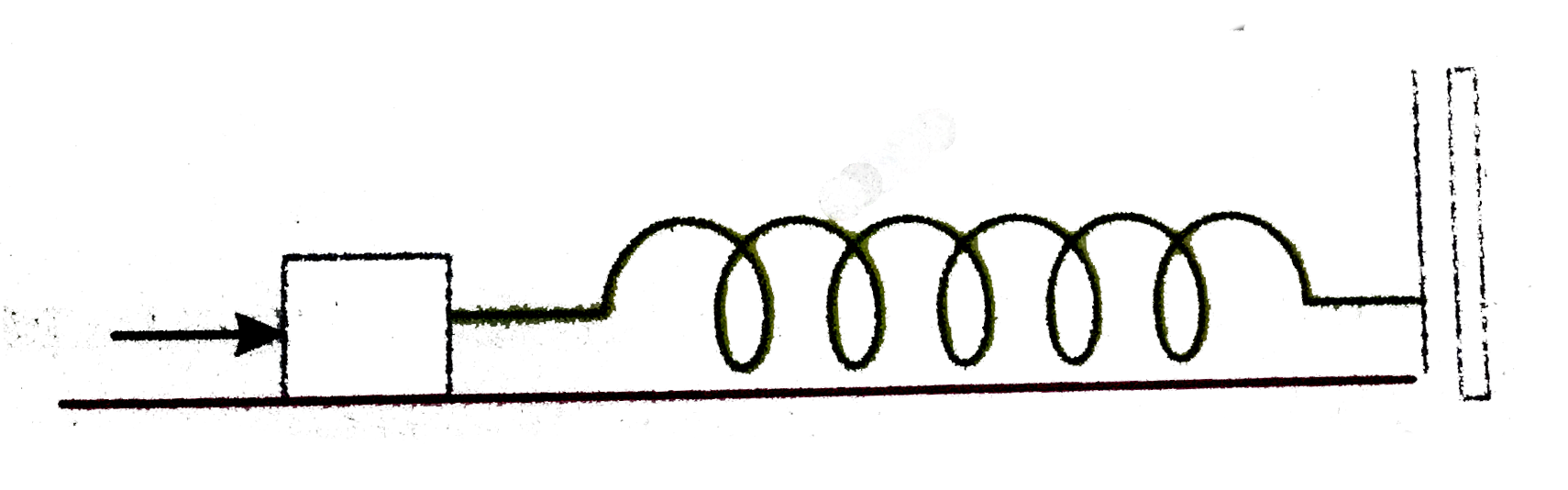 .
.
View SolutionA block of mass 1 kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5, magnitude of the frictional force acting on the block is
View SolutionA block of mass m=4kg is placed over a rough inclined plane as shown in fig . The coefficient of friction between the block and the plane μ=0.5 A force F=10N is applied on the block at an angle of 30∘. Find the contact force between the block and the plane.
k

View SolutionA small block of mass m is projected on a larger block of mass 10m and length l with a velocity v as shown in the figure. The coefficient of friction between the two block is μ2 while that between the lower block and the ground is μ1. Given that μ2>11μ1.

(a) Find the minimum value of v, such that the mass m falls off the block of mass 10m .
(b) If v has minimum value, find the time taken by block m to do so.
View Solution
