A block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
Here, m=20g,M=180g,h=2m,k=120N/m
The velocity of ball after falling h,
v0=√2gh=√2×10×20=20m/s
Applying momentum conservation between (B) and (C) ltbrlt mv0=(m+M)v⇒20×20=(20+180)v⇒v=2m/s
Let the maximum compression of the spring be x.
Applying the energy conservation between (C) and (D)
12(m+M)v2+(m+M)gx=12kx2
12×0.2×(2)2+0.2×10x=12×120x2
60x2−2x−0.4=0
x=2±√4+4×60×0.4120=2±10120
x=12120=0.1m=10cm

Topper's Solved these Questions
Similar Questions
A block of mass 180g is suspended by a massless spring. The spring extends by 1.8cm due to the weight of block. A particle of mass 20g is dropped from a height 80cm on the block. The collision is completely inelastic . Find the maximum elongation of the spring.
View SolutionThe ball strikes the block and sticks to it. Find the maximum compression of spring. (L: natural length of spring)

View Solution
Knowledge Check

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
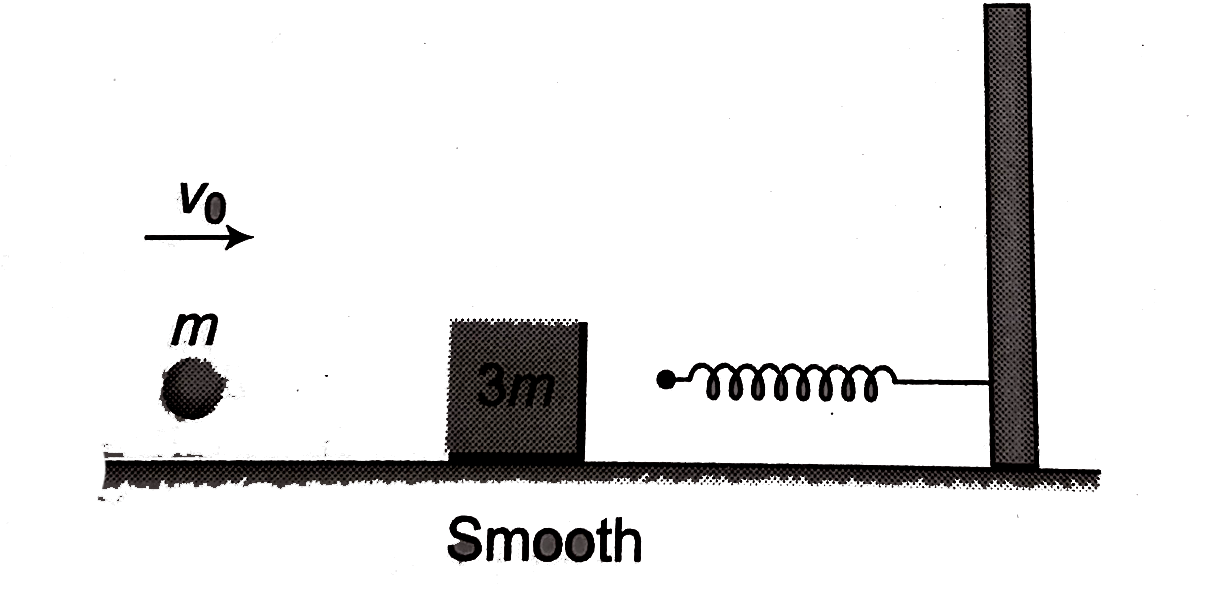 A√mv20kB√mv202kC√mv203kD√mv204k
A√mv20kB√mv202kC√mv203kD√mv204kA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View Solution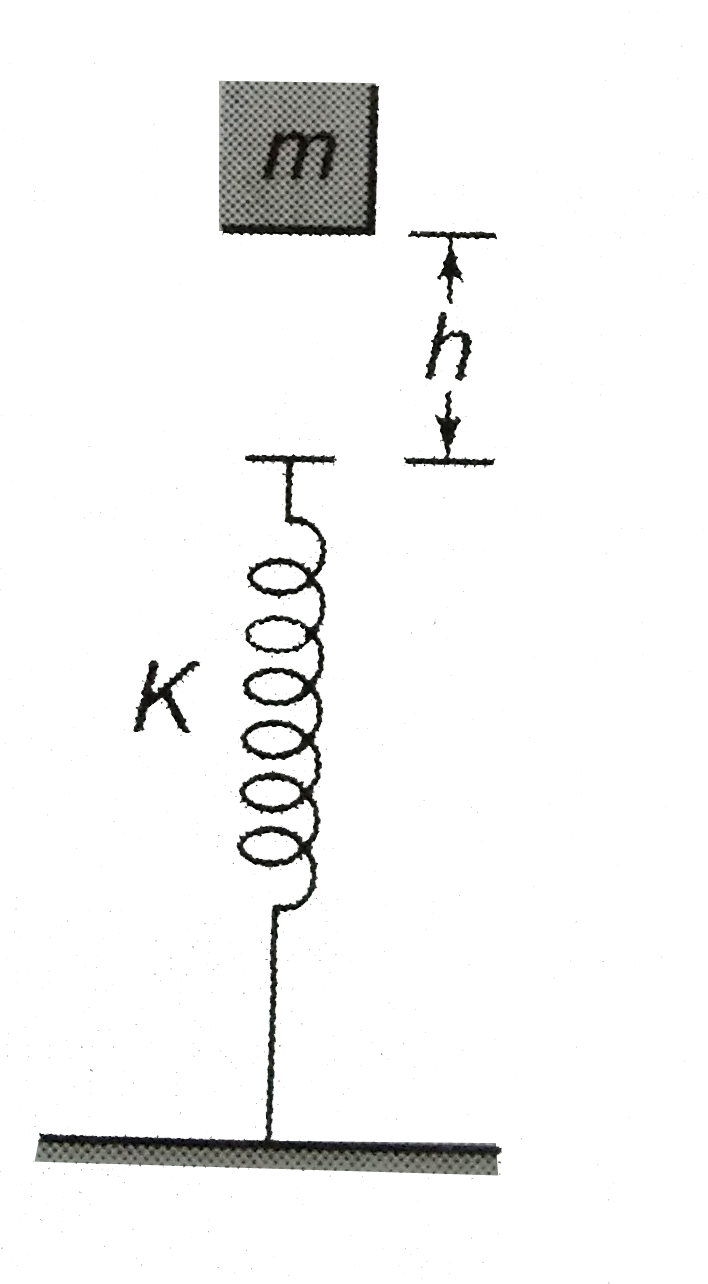
A block is released from height h, find the maximum compression of spring of spring constant k.
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View SolutionA block of mass m = 2.0 kg is dropped from height h = 40 cm onto a spring of spring constant k=1960N/s. Find the maximum distance through which the spring is compressed. Take g=9.8m/s2
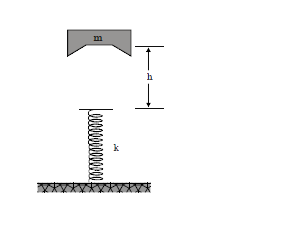
View Solution
