A block of mass 200 gm is suspended through a vertical spring. The spring is stretched by 1 cm when the block is in equilibrium. A particle of mass 120 gm is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring.
The correct Answer is:[6.1cm]
To solve the problem step by step, we will follow these steps:
Step 1: Understand the System
We have a block of mass m1=200g=0.2kg suspended from a spring. The spring stretches by x1=1cm=0.01m when the block is in equilibrium. A second mass m2=120g=0.12kg is dropped from a height of h=45cm=0.45m and sticks to the block upon impact.
Step 2: Calculate the Force on the Spring
The force exerted by the block on the spring at equilibrium can be calculated using the formula:
F=m1⋅g
where g≈9.81m/s2.
Calculating this gives:
F=0.2⋅9.81=1.962N
Step 3: Determine the Spring Constant
Using Hooke's Law, which states that F=k⋅x, we can find the spring constant k:
k=Fx1=1.9620.01=196.2N/m
Step 4: Calculate the Velocity of the Dropped Mass Just Before Impact
The velocity of the mass m2 just before it hits the block can be found using the equation of motion:
v=√2gh
Substituting the values:
v=√2⋅9.81⋅0.45≈√8.829≈2.97m/s
Step 5: Apply Conservation of Momentum
When the mass m2 sticks to m1, we can use the conservation of momentum:
m2⋅v=(m1+m2)⋅V
where V is the velocity of the combined mass after the collision. Rearranging gives:
V=m2⋅vm1+m2
Substituting the values:
V=0.12⋅2.970.2+0.12=0.35640.32≈1.11m/s
Step 6: Calculate the Maximum Extension of the Spring
At maximum extension, all the kinetic energy will be converted into potential energy stored in the spring. The kinetic energy just after the collision is:
KE=12(m1+m2)V2
Substituting the values:
KE=12⋅(0.2+0.12)⋅(1.11)2≈12⋅0.32⋅1.2321≈0.196J
The potential energy stored in the spring at maximum extension x is given by:
PE=12kx2
Setting KE=PE:
0.196=12⋅196.2⋅x2
Solving for x2:
x2=0.196⋅2196.2≈0.001m2
Thus,
x≈0.0316m=3.16cm
Final Answer
The maximum extension of the spring is approximately 3.16cm.
---
We have a block of mass m1=200g=0.2kg suspended from a spring. The spring stretches by x1=1cm=0.01m when the block is in equilibrium. A second mass m2=120g=0.12kg is dropped from a height of h=45cm=0.45m and sticks to the block upon impact.
The force exerted by the block on the spring at equilibrium can be calculated using the formula:
F=m1⋅g
where g≈9.81m/s2.
F=0.2⋅9.81=1.962N
Using Hooke's Law, which states that F=k⋅x, we can find the spring constant k:
k=Fx1=1.9620.01=196.2N/m
The velocity of the mass m2 just before it hits the block can be found using the equation of motion:
v=√2gh
Substituting the values:
v=√2⋅9.81⋅0.45≈√8.829≈2.97m/s
When the mass m2 sticks to m1, we can use the conservation of momentum:
m2⋅v=(m1+m2)⋅V
where V is the velocity of the combined mass after the collision. Rearranging gives:
V=m2⋅vm1+m2
Substituting the values:
V=0.12⋅2.970.2+0.12=0.35640.32≈1.11m/s
At maximum extension, all the kinetic energy will be converted into potential energy stored in the spring. The kinetic energy just after the collision is:
KE=12(m1+m2)V2
Substituting the values:
KE=12⋅(0.2+0.12)⋅(1.11)2≈12⋅0.32⋅1.2321≈0.196J
PE=12kx2
Setting KE=PE:
0.196=12⋅196.2⋅x2
Solving for x2:
x2=0.196⋅2196.2≈0.001m2
Thus,
x≈0.0316m=3.16cm
The maximum extension of the spring is approximately 3.16cm.
Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - exercise 1.3
3 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Advance McQ
20 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
A block of mass 200 g is suspended by a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g=10m/s2.

View SolutionA block of mass 180g is suspended by a massless spring. The spring extends by 1.8cm due to the weight of block. A particle of mass 20g is dropped from a height 80cm on the block. The collision is completely inelastic . Find the maximum elongation of the spring.
View Solution
Knowledge Check
A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionThe ball strikes the block and sticks to it. Find the maximum compression of spring. (L: natural length of spring)

View SolutionA block of mass m is suspened through a spring of spring constant k and is in equlibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium psitin, the block comes to an instantaneous rest?
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
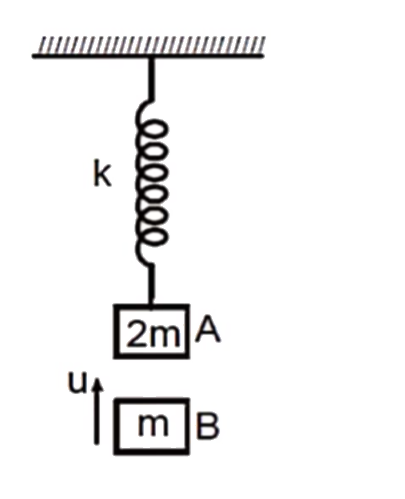
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
