A block of mass 5 kg moves from left to right with a velocity of 2ms−1 and collides with another block of mass 3 kg moving along the same line in the opposite direction with velocity 4ms−1.
(i) If the collision is perfectly elastic, determine velocities of both the blocks after their collision.
(ii) If coefficient of restitution is 0.6, determine velocities of both the blocks after their collision.
Denoting the first block by A and the second block by B velocities immediately before and after the impact are shown in the figure.
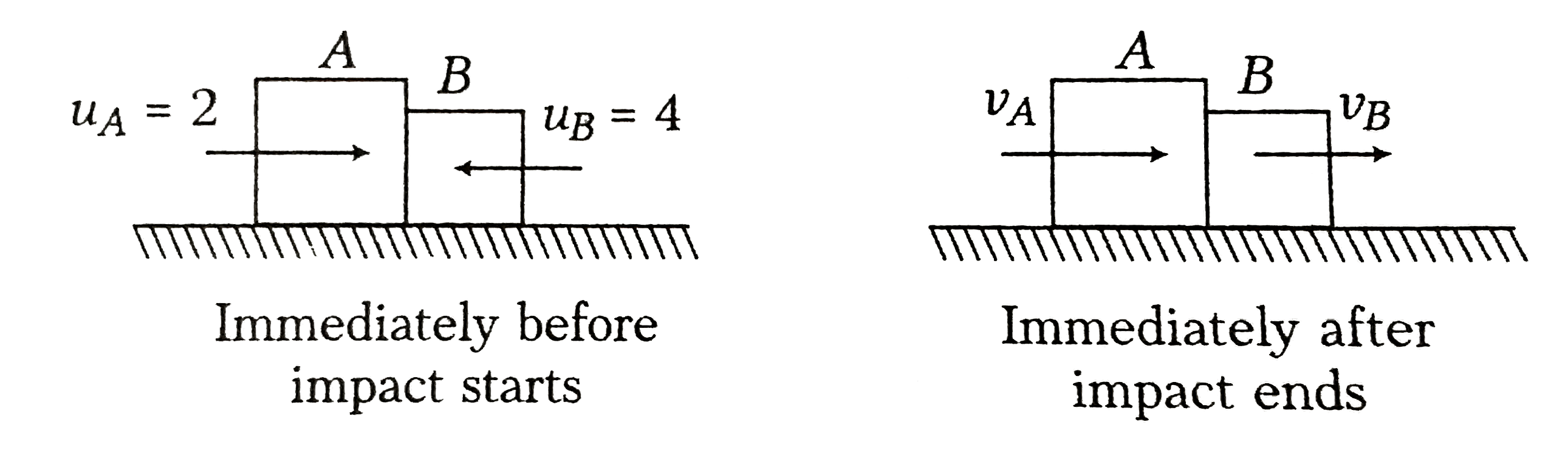
Applying principle of conservation of momentum, we have
⇒(mBvB+mAvA=mAuA+mBuB)
3vB+5vA=5×2+3×(−4)
3vB+5vA=−2.............(i)
Applying equation of coefficient of resolution, we have
vA−vB=e(uA−uB)
⇒vB−vA=e[2−(−4)]
vB−vA=6e ...................(ii)
(i) For perfectly elastic impact e=1. Using this value in Eq. (ii), we have
vB−vA=6..................(iii)
Now , from Eqs. (i) and (iii), we obtain
vA=−2.5ms−1 and vB=3.5ms−1
(ii) For value e = 0.6, Eq. (ii) is modified ias
vB−vA=3.6 ..................(iv)
Now from Eqs. (i) and (iv), we obtain
vA=−1.6ms−1 and vB=2ms−1
Block A reverse back with speed 1.6ms−1 and B also move in opposite direction to its original direction with speed 2ms−1
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A block of mas m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of te blocks after the collision.
View SolutionA body of mass 3kg moving with a velocity of 4m/s towards left collides head on with a body of mass 4kg moving in opposite direction with a velocity of 3m/s. After collision the two bodies stick together and move with a common velocity which is
View Solution
Knowledge Check
A ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
Aboth the balls come to restBthe velocities are exchanged between the two ballsCboth of them move at right angles to the original line of motionDone ball comes to rest and another ball travels back with velocity 2vA body of mass 1 kg moving with velocity 5 m/s collides with another body of mass 2 kg moving with velocity 1.5 m/s in opposite direction. If the coefficient of restitution is 0.8, their velocities aftter collision respectively are
A−2.8 m/s,+2.4 m/sB+2.8 m/s,−2.4 m/sC−1.67 m/s,−2.4 m/sD+2.8 m/s,−6.84 m/sA body of mass 4kg moving with a speed of 3ms−1 collides head on with a body of mass 3kg moving in the opposite direction at a speed of 2ms−1. The first body stops after the collision. The final velocity of the second body is
A3ms−1B5ms−1C−9ms−1D30ms−1
A body of mass 2kg moving with a velocity of 3m/sec towards left collides head-on with a body of mass 3kg moving in opposite direction with a velocity 2m/sec. After collision the two bodies stick together and move with a common velocity which is :
View SolutionA ball of mass 10 kg is moving with a velocity of 10 m / s . It strikes another ball of mass 5 kg which is moving in the same direction with a velocity of 4 m / s . If the collision is elastic, their velocities after the collision will be, respectively
View SolutionA body of mass 2 kg moving with a velocity 3m/sec collides with a body of mass 1 kg moving with a velocity of 4m/sec in opposite direction. If the collision is head-on perfect inelastic, then
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View SolutionA ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
View Solution
