A block of mass M connected to an ideal spring of force constant k, is placed on a smooth surface. The block is pushed to the left so as to compress the spring by a length A and then it is released. The block hits an elastic wall at a distance 3A2 from its point of release. Assume the collision to be instantaneous.
(a) Calculate the time required by the block to complete one oscillation
(b) Draw the velocity - time graph for one oscillation of the block.
(c) Find the value of k for which average force experienced by the wall due to repeated hitting of the block is F0.
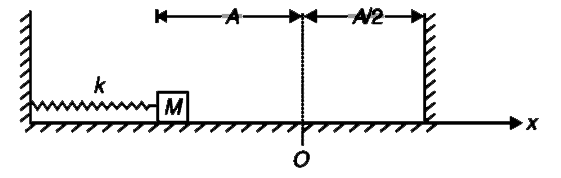
The correct Answer is:(a)4π3√Mk, (b) (##IJAPHYV01C12E01033_A01##)
(c ) k=4πF03√3A
Step by step video, text & image solution for A block of mass M connected to an ideal spring of force constant k, is placed on a smooth surface. The block is pushed to the left so as to compress the spring by a length A and then it is released. The block hits an elastic wall at a distance (3A)/(2) from its point of release. Assume the collision to be instantaneous. (a) Calculate the time required by the block to complete one oscillation (b) Draw the velocity - time graph for one oscillation of the block. (c) Find the value of k for which average force experienced by the wall due to repeated hitting of the block is F_(0). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- ROTATIONAL MOTIONBOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159 Videos
- SURFACE TENSIONBOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension
33 Videos
Similar Questions
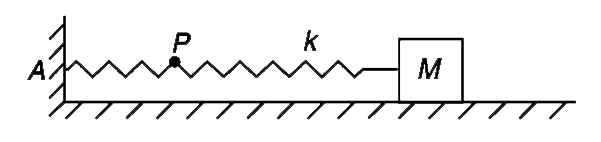
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
Knowledge Check
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ thenAMotion of block is SHMBTime period of motion is π√mk[√2+√23]CTime period of motion is π√mk[1+√32]DSum of potential energy and kinetic energy of spring block system is maximum at right extreme.Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
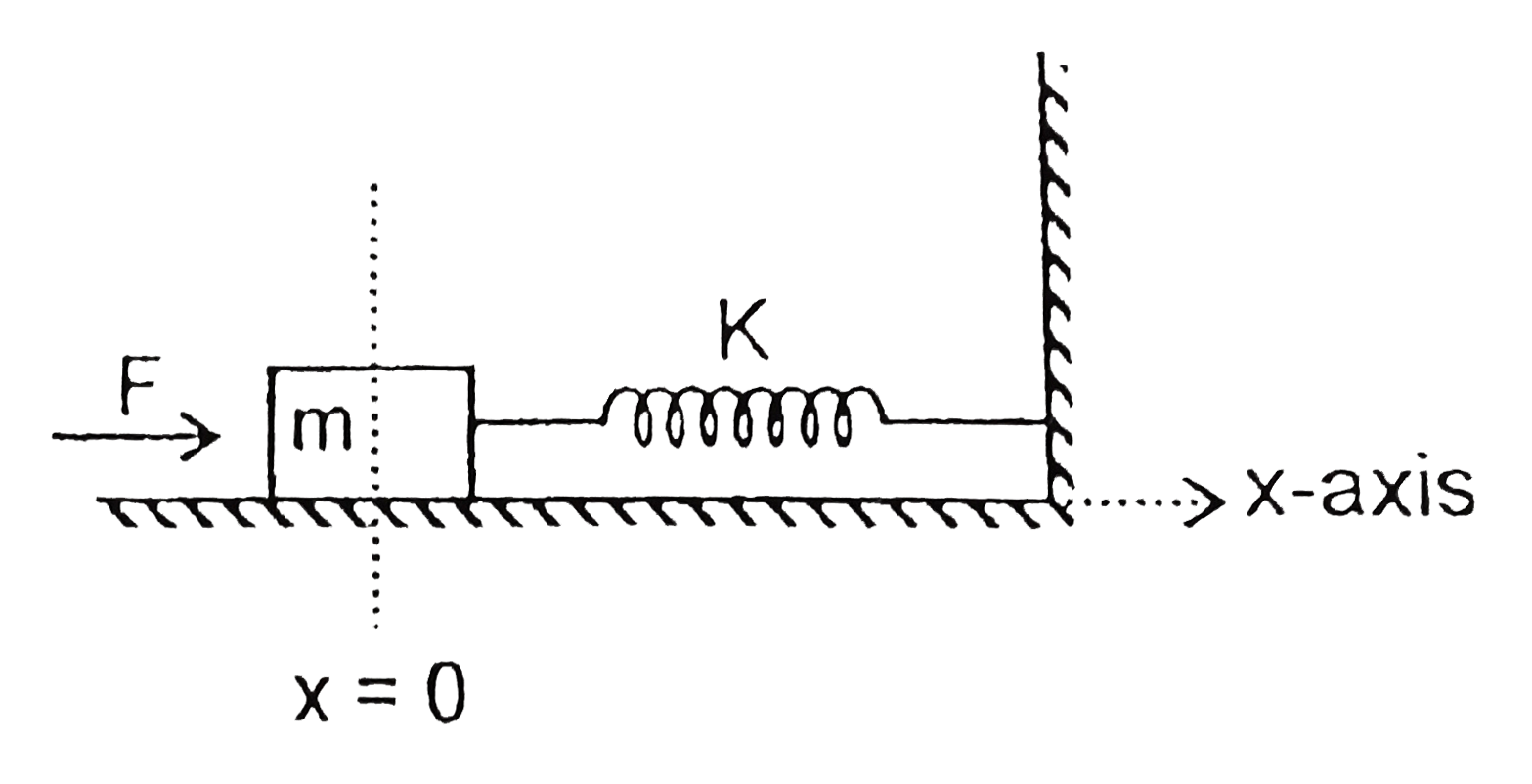
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correctA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
Ax=√mkBa=1v√mkCx=v√mkDx=√mvk
Two blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View SolutionA block of mass m is attached to two unstretched springs of spring constant k1 and k2 as shown in figure. The block is displaced towards right through a distance 'x' and is released. Find the speed of the block as it passes through a distance x/4 from its mean position. All the surfaces are smooth.
View SolutionA spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to x0 and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface There is another and wall at a distance x0 from the block The spring is then compressed by 2x0 and released The time taken to at the wall is
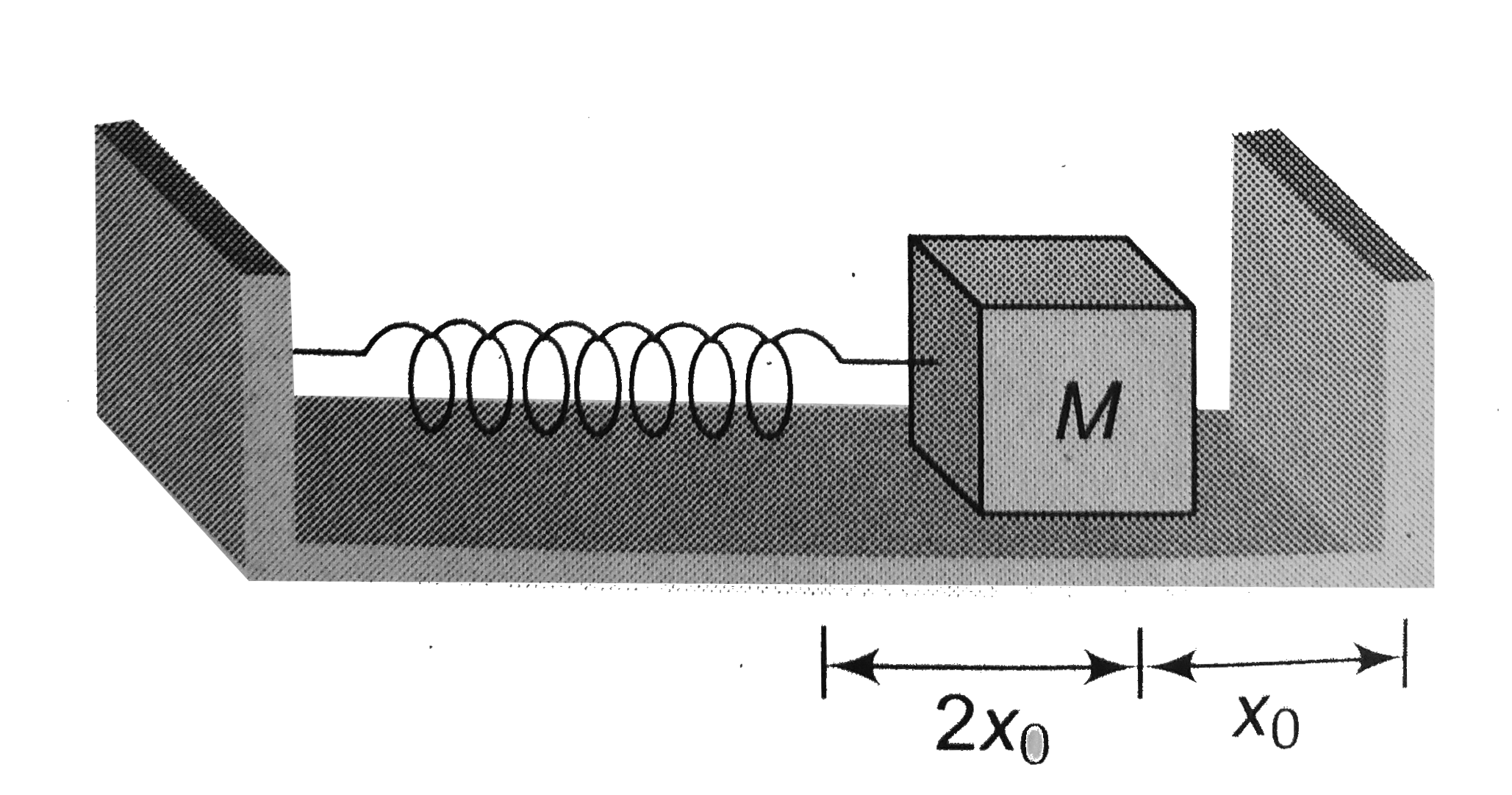
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View Solution
