A block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
tan−1(μ/m)
tan−1(μ)
tan−1(μ/2)
cos−1(μ)
The correct Answer is:B
To solve the problem of finding the maximum angle of incline (θ) before a block of mass m begins to slide down, we can follow these steps:
1. Identify Forces Acting on the Block:
- The weight of the block (mg) acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
2. Determine the Normal Force (N):
- The normal force (N) acting on the block is equal to the perpendicular component of the weight:
N=mgcosθ
3. Calculate the Frictional Force (F_f):
- The maximum static frictional force that can act on the block is given by:
Ff=μN=μ(mgcosθ)
4. Set Up the Condition for Sliding:
- The block will start to slide when the component of gravitational force parallel to the incline equals the maximum static frictional force:
mgsinθ=μ(mgcosθ)
5. Simplify the Equation:
- Cancel mg from both sides (assuming m≠0):
sinθ=μcosθ
6. Divide Both Sides by cosθ:
- This gives us:
tanθ=μ
7. Find the Angle θ:
- To find the angle θ, take the inverse tangent:
θ=tan−1(μ)
Final Answer:
The maximum angle of incline before the block begins to slide down is:
θ=tan−1(μ)
- The weight of the block (mg) acts vertically downward.
- This weight can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
- The normal force (N) acting on the block is equal to the perpendicular component of the weight:
N=mgcosθ
- The maximum static frictional force that can act on the block is given by:
Ff=μN=μ(mgcosθ)
- The block will start to slide when the component of gravitational force parallel to the incline equals the maximum static frictional force:
mgsinθ=μ(mgcosθ)
- Cancel mg from both sides (assuming m≠0):
sinθ=μcosθ
- This gives us:
tanθ=μ
- To find the angle θ, take the inverse tangent:
θ=tan−1(μ)
The maximum angle of incline before the block begins to slide down is:
θ=tan−1(μ)
Topper's Solved these Questions
- SAMPLE QUESTION PAPER 4BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 4EXERCISE - SECTION - B (Answer all questions.)
13 Videos
- SAMPLE QUESTION PAPER 4BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 4EXERCISE - SECTION - C (Answer all questions.)
9 Videos
- SAMPLE QUESTION PAPER - 01 BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER - 01 EXERCISE - SECTION - D
12 Videos
- SAMPLE QUESTION PAPER 5BOOK - ICSECHAPTER - SAMPLE QUESTION PAPER 5EXERCISE - SECTION - D (Answer all questions.)
6 Videos
Similar Questions
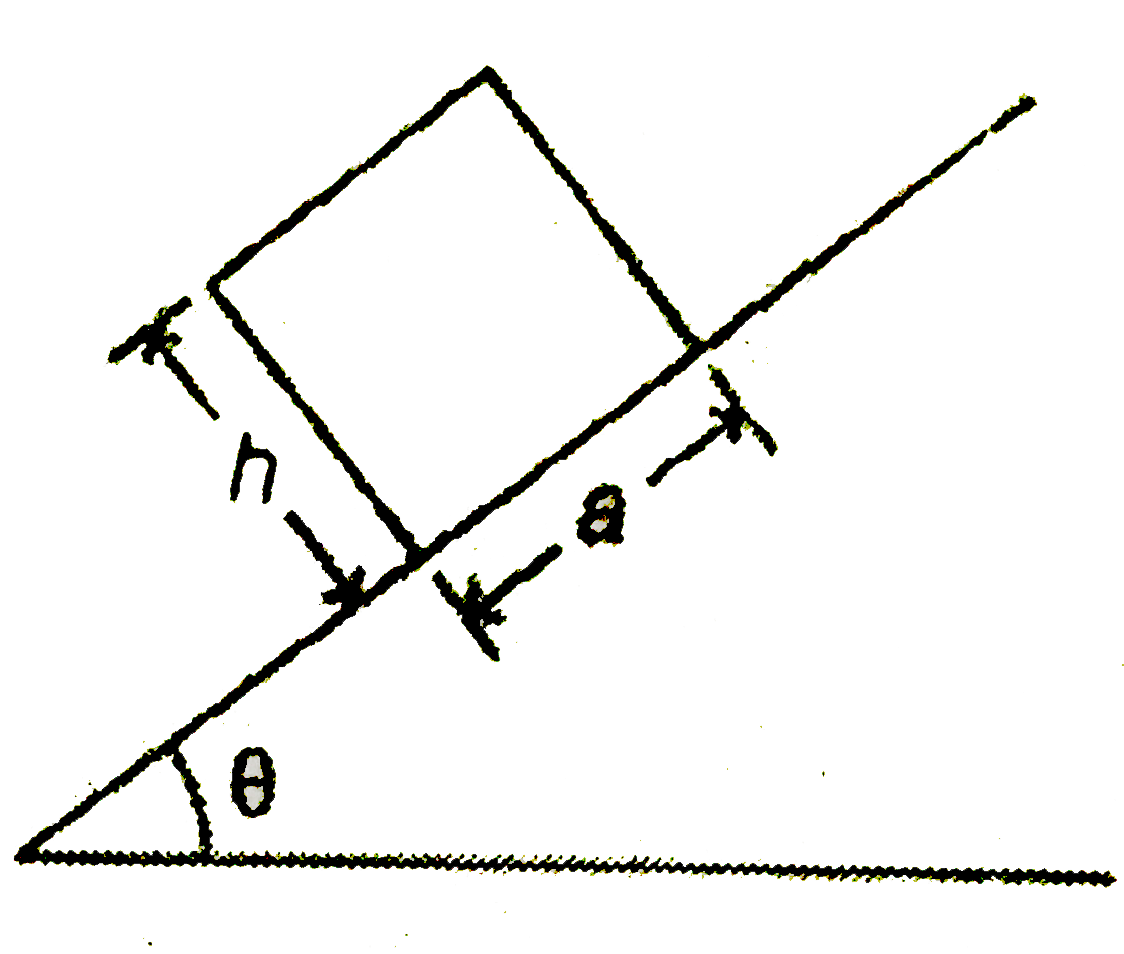
A block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
View SolutionA block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block

View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μA block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

View Solution
