A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
2mgμk
mgμk
4mgμk
None of these
The correct Answer is:C
Ei−Ef= Work done againt fricion
∴12kx2−12K(x2)2=μmg(x+x2)
∴x=4μmgk.
Similar Questions
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
Knowledge Check
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
AThe spring was initially compessed by a distance x and was finally in its natural length .BIt was initially stretched by a distance x and finally was in its natural length.CIt was initially natural length and finally in a compressed position.DIt was initially in its natural length and finally in a stretched position.
A block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck

View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View SolutionTwo block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
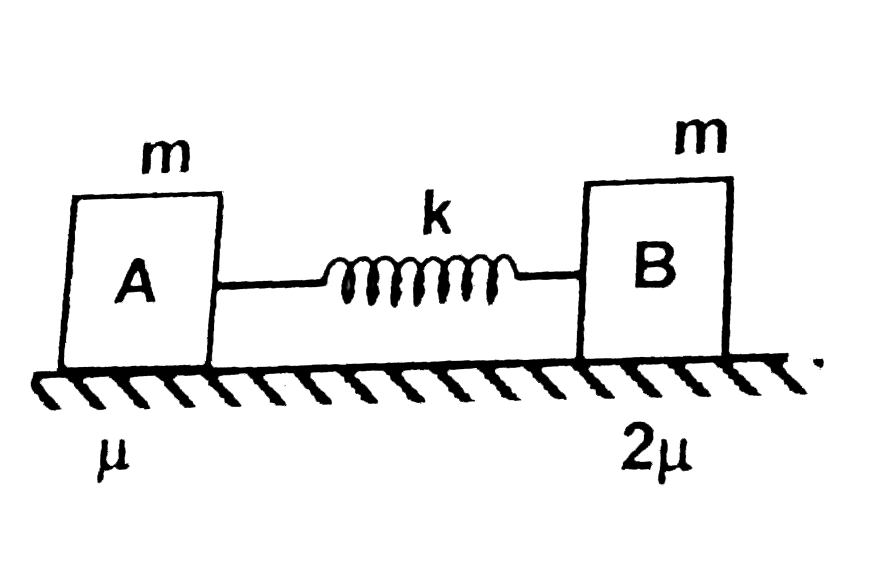
View Solution
