A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

The correct Answer is:B
The centre of mass of the system (two blocks+spring) moves with an acceleration a=Fm+M. Let us solve the problem in a frame of reference fixed to the centre of mass of the system. As this frame is accelerated with respect to the ground, we have to apply a pseudo force ma towards left on the block of mass m and Ma towards left on the block of mass M. The net external force on m is
F1=ma=mFm+M (towards left)
and the net external force on M is
F2=F−Ma=F−MFm+M=mFm+M (towards right)
As the centre of mass is at rest in this frame, the blocks move in opposite directions and come to instantaneous rest at some instant. The extension of the spring will be maximum at this instant. Suppose, the left block is displaced through a distance x1 and the right block through a distance x2 from the initial positions. The total work done by the external force F1 and F2 in this period are
W=F1x1+F2x2=mFm+M(x1+x2)
This should be equal to the increase in the potential energy of the spring, as there is no change in the kinetic energy. Thus,
mFm+M(x1+x2)=12k(x1+x2)2 or x1+x2=2mFk(m+M)
This is the maximum extension of the spring.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.1
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.2
6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A block of mass m is connected to another block of mass M by a massless spring of spring constant k. the blocks are kept of a smooth horizontal plane and are at rest. The spring is unstretched when a constant force F starts acting on the block of mass M of pull it. Find the maximum extension of the spring
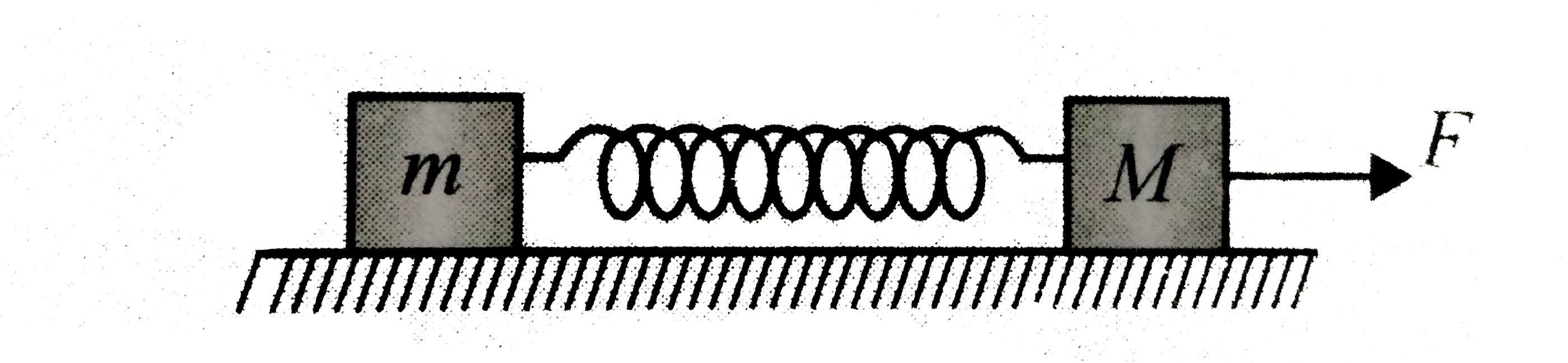
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View Solution
Knowledge Check
A block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
A(a) MF(m+M)B(b) mFMC(c) (M+m)FmD(d) mF(m+M)A block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
AMF(m+M)BmFMC(M+m)FmDmF(m+M)A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of these
A block of mass m is connected to another block of mass M by a massless spring of spring constant K. Blocks are kept on a smooth horizontal plane. Initally both the blocks the at rest and spring is unstressed. Force F is applied on M to right as shownin the figure then which of the following is correct ?

View SolutionInitially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
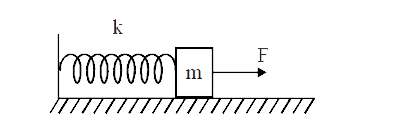
maximum extension in the spring
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
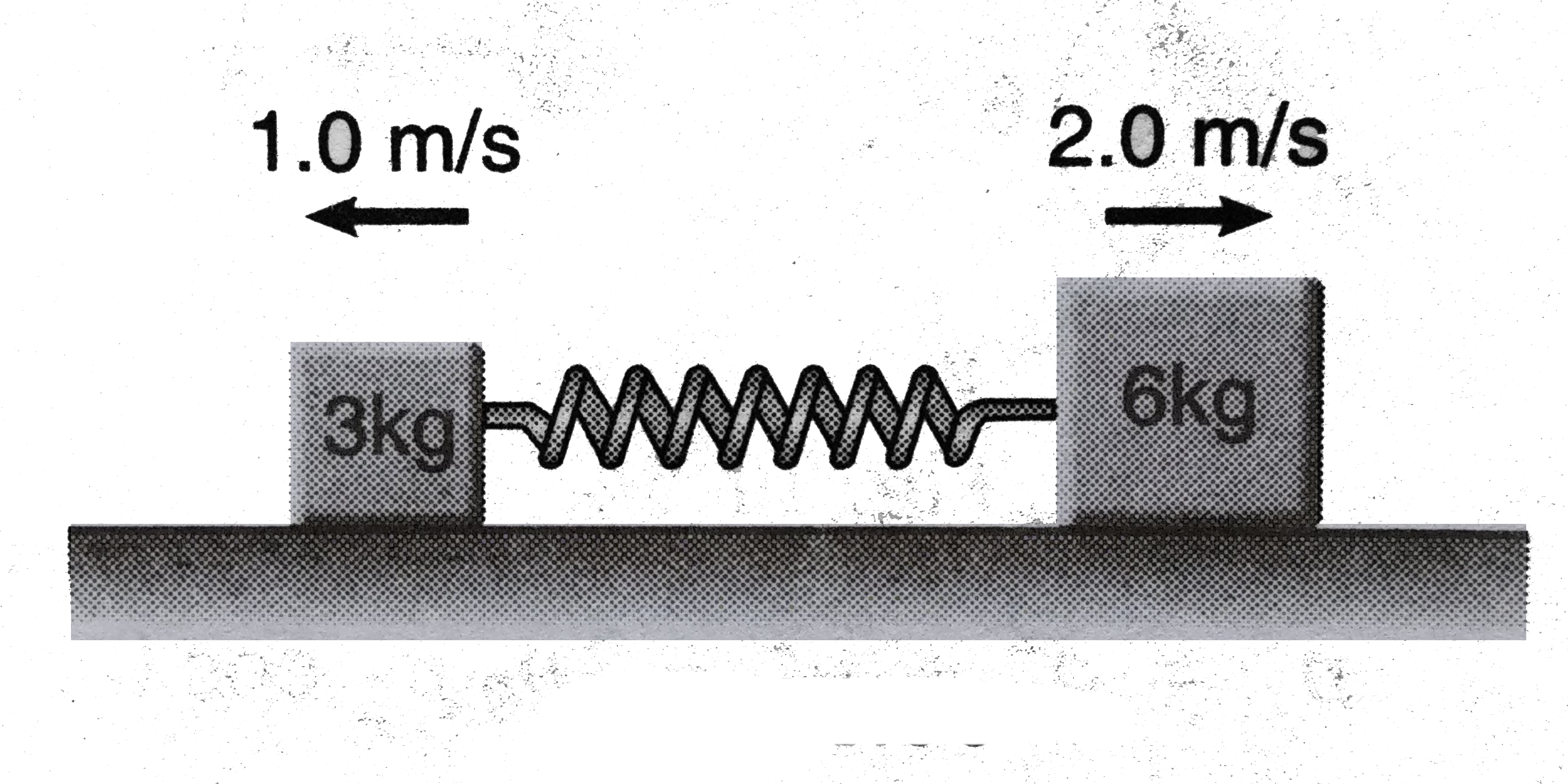
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
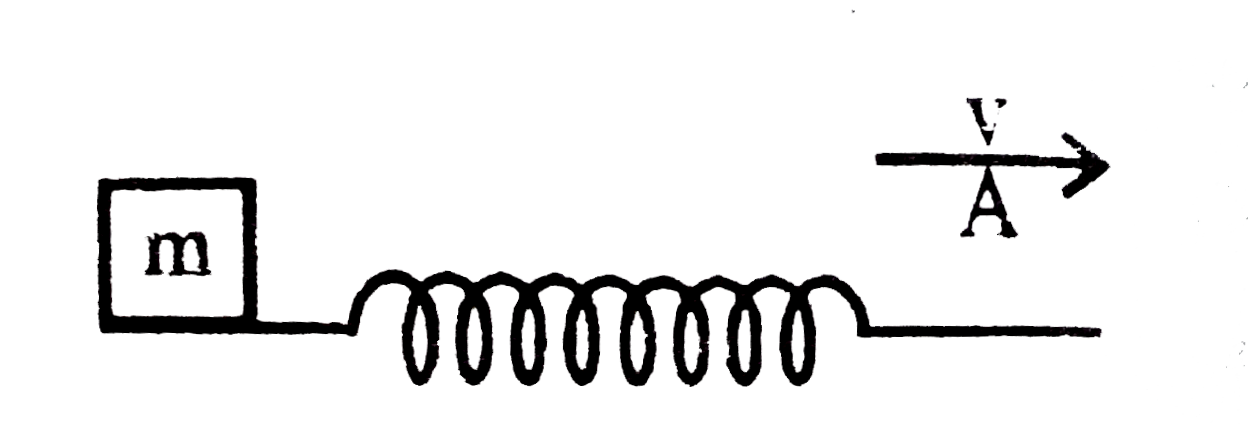
View Solution
