A block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be

π2√Mk
2π√M5k
3π2√Mk
π√M2k
The correct Answer is:C
Half the oscillation is completed with one spring and the other half with other spring. Hence,
T=T12+T22=2π√(M)k2+2π√(M)4k2
=π√Mk[1+12]=3π2√Mk
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
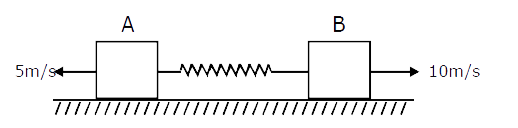
The two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
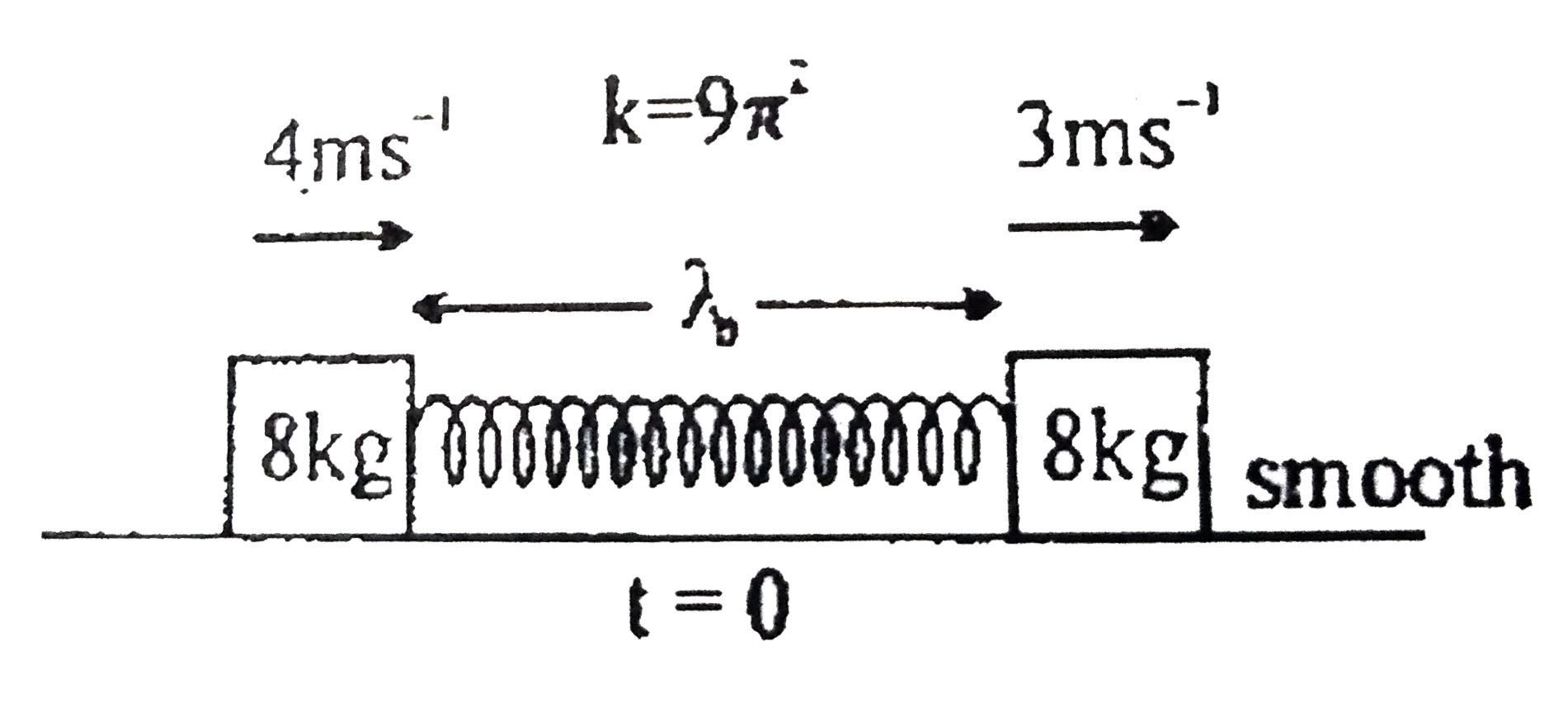
View SolutionTwo block-spring mass system are moving on smooth horizontal surface as shown in the figure as t=0. find out the minimum time t when the spring is maximum elongated l0 is the natural length of spring.
View Solution
Knowledge Check
A block of mass m is attached to the two springs in vertical plane as shown in the figure - 3.95. If initially both the springs are at their natural lengths then velocity of the block is maximum at displacement x given as
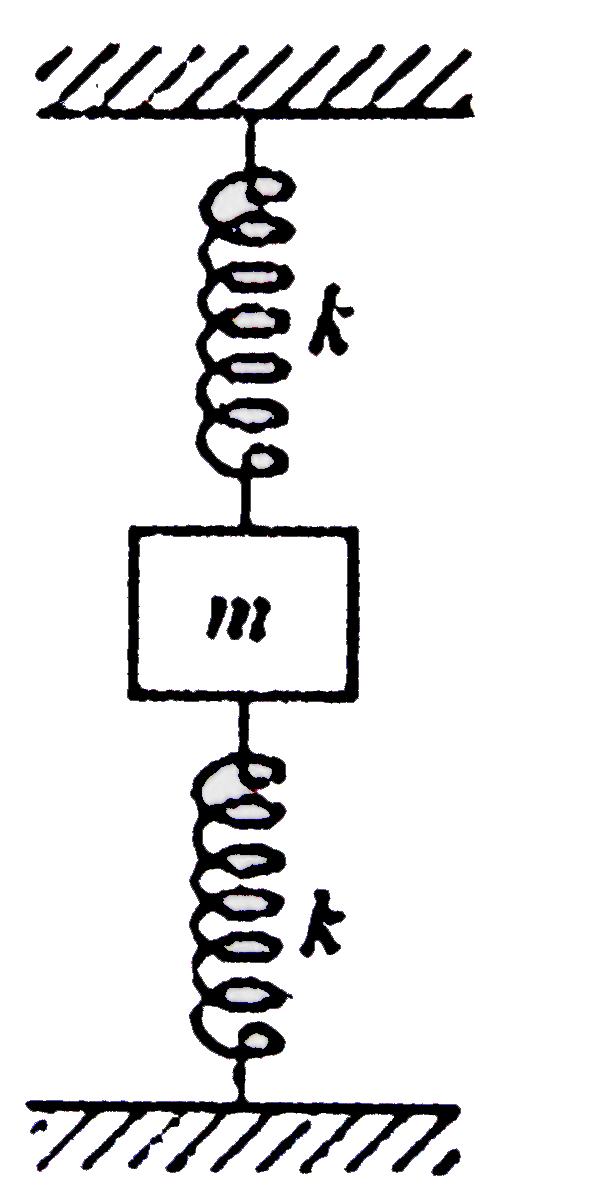 Ax=mg2kBx=mgkCx=mg4kDx=3mg2k
Ax=mg2kBx=mgkCx=mg4kDx=3mg2kA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
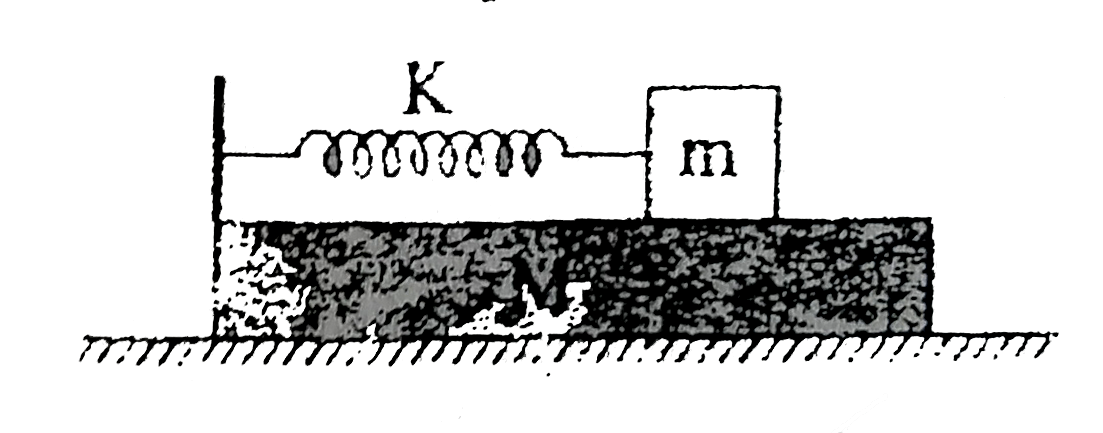 A√m2KV0B√mKv0C√2mKv0D2√mKv0
A√m2KV0B√mKv0C√2mKv0D2√mKv0A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
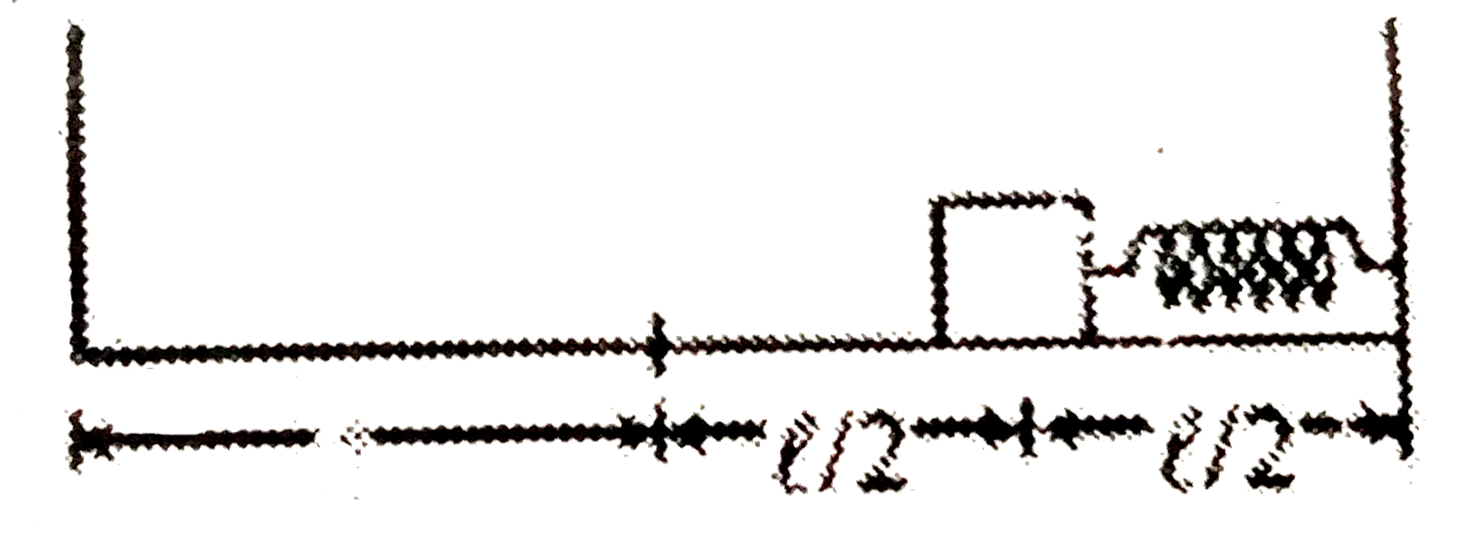
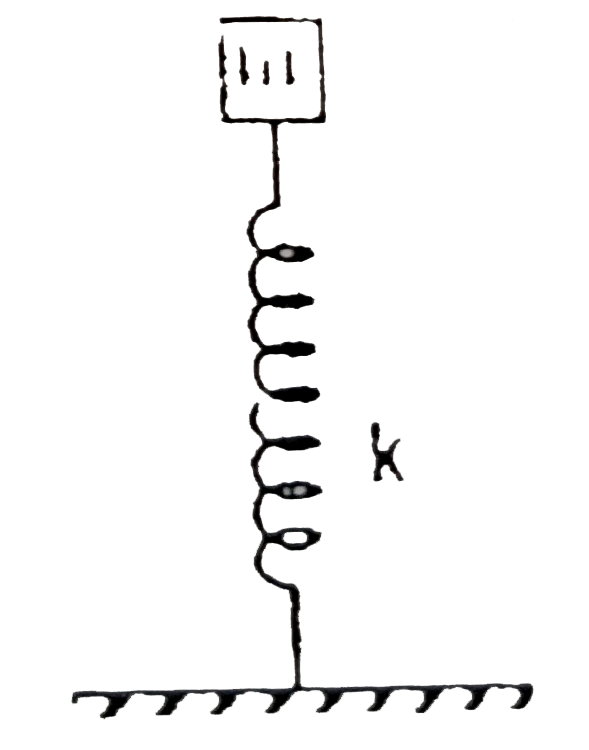
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
View SolutionIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be

View Solution