A block of mass m is on an inclined plane of angle e. The coefficient of friction between the block and the plane is and . The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from to , the frictional force f versus P graph will look like.





The correct Answer is:a
Here :
so linear decreasing graph with value ranging from mu mg cos theta to - mu mg cos thetais the right choice.
Hence (a) is the correct choice.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - MULTIPLE CHOICE QUESTION (LEVEL-III)
2 Videos
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - RECENT COMPETITIVE QUESTIONS
7 Videos
- LAWS OF MOTIONBOOK - MODERN PUBLICATIONCHAPTER - LAWS OF MOTIONEXERCISE - Revision test
43 Videos
- HEAT AND THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - Recent Competitve Questions
17 Videos
- MAGNETOSTATICSBOOK - MODERN PUBLICATIONCHAPTER - MAGNETOSTATICSEXERCISE - RECENT COMPETITIVE QUESTION
5 Videos
Similar Questions
Knowledge Check
A block of mass m is on an inclined plane of angle θ. The coefficient of friction between the block and the plane is μ and tanθ>μ. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from P1=mg(sinθ−μcosθ) to P2=mg(sinθ+μcosθ), the frictional force f versus P graph will look like
A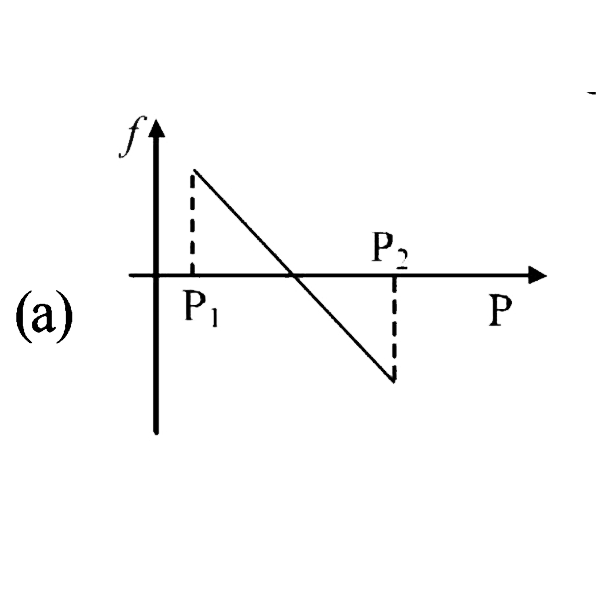 B
B C
C D
D
A block of mass m is on an inclined plane of angle θ. The coefficient of friction between the block and the plane is μ and tanθ>μ. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from P1=mg(sinθ−μcosθ) to P2=mg(sinθ+μcosθ), the frictional force f versus P graph will look like
A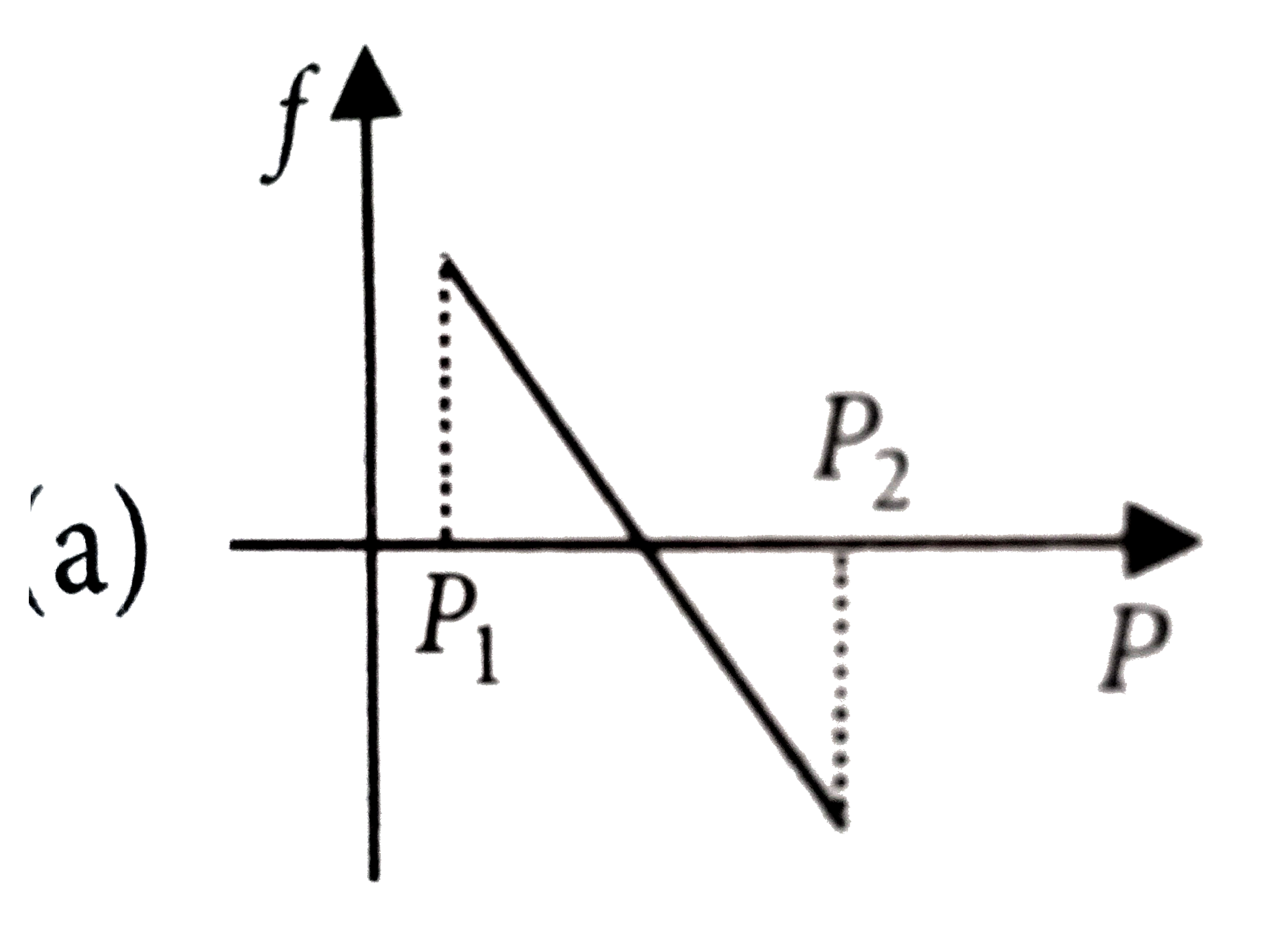 B
B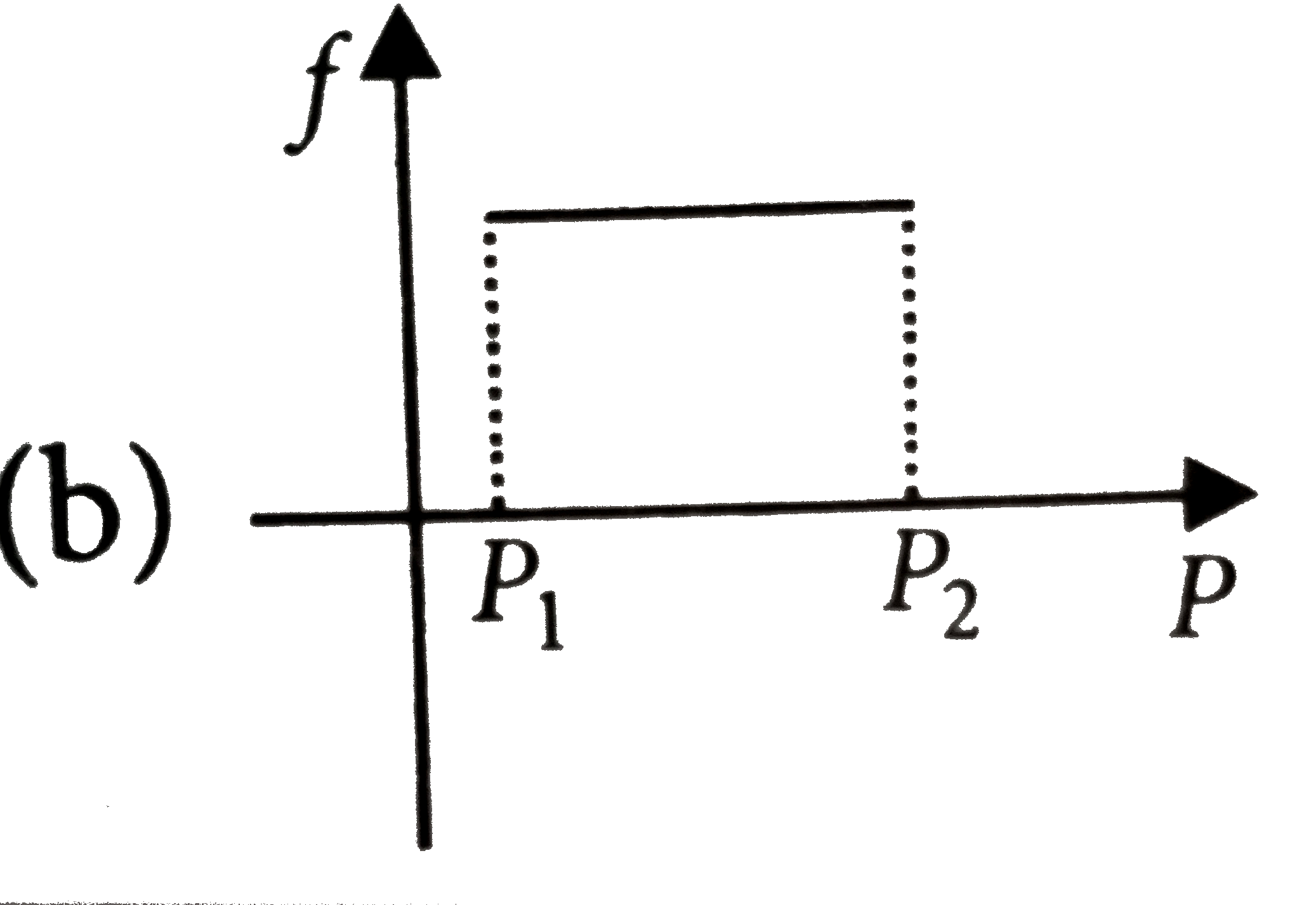 C
C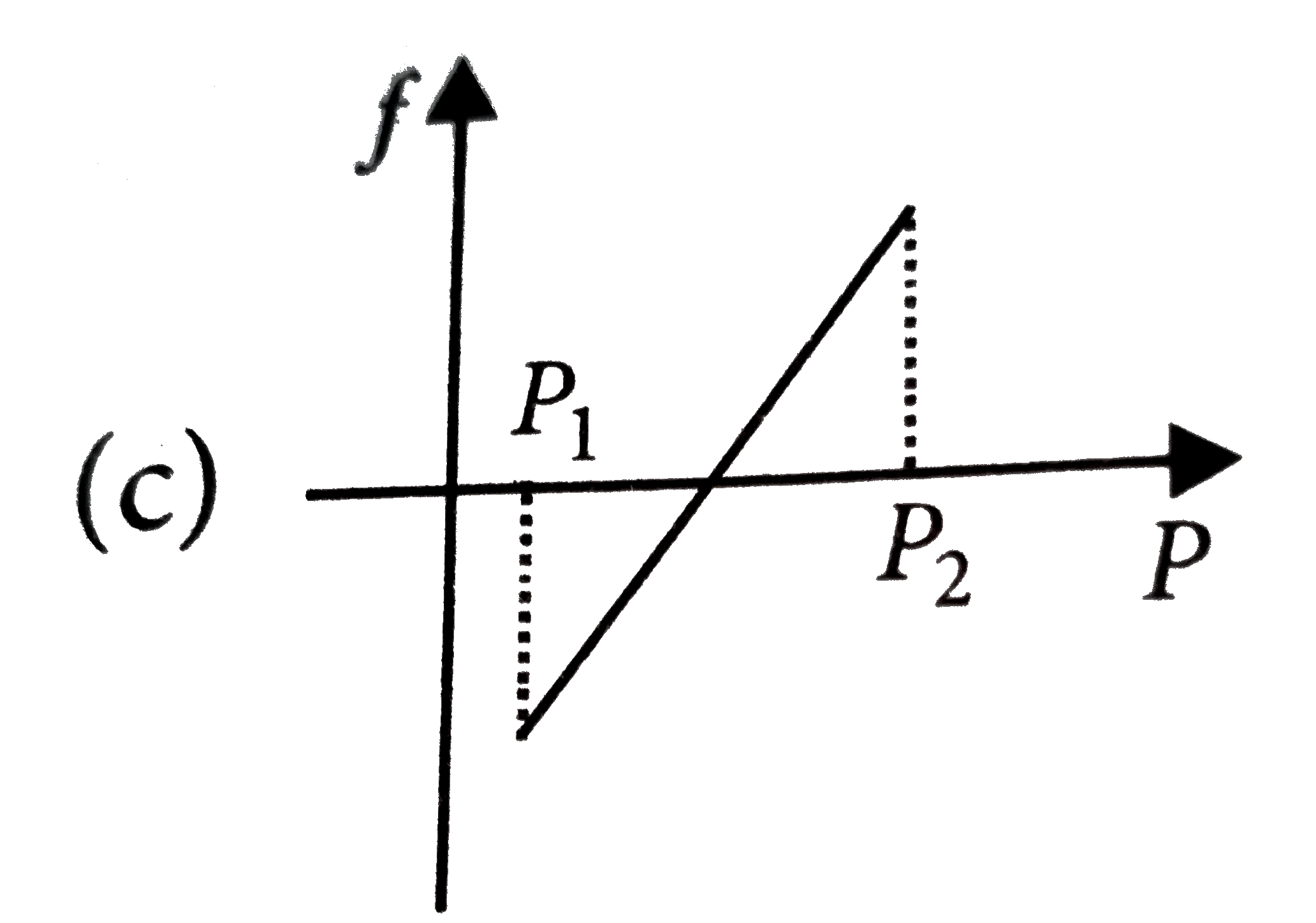 D
D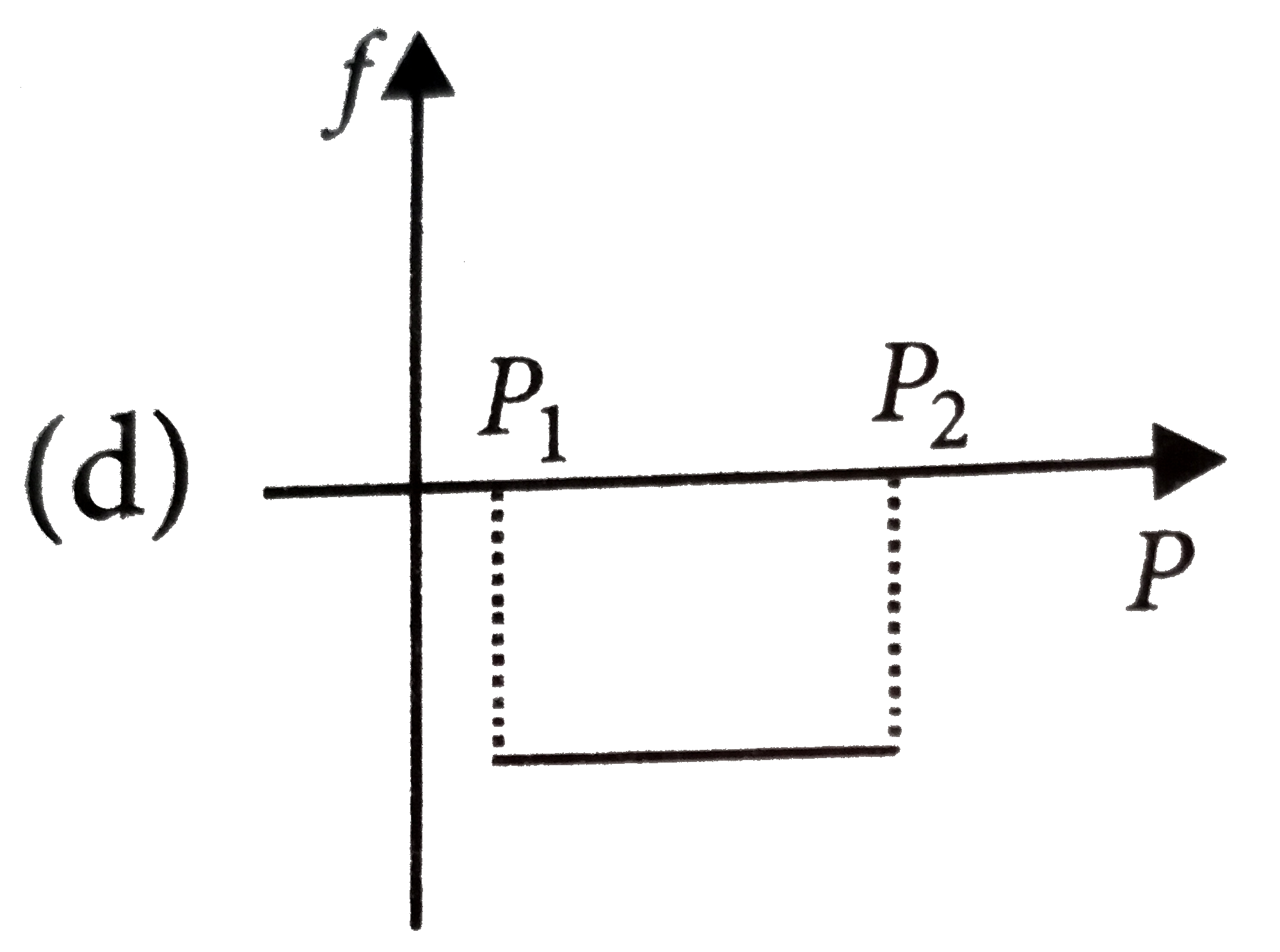
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View Solution
