A block of mass m is slowly lowered from a point where it just touches a vertical fixed spring of stiffness k, till it remains stationary after the applied force is withdrawn. Find the work done by the external agent(a) in compressing the spring by a distance x and (b) bringing the block to its stable equilibrium position.

a. As the block is moving down, the spring pushes it up with a force Fsp=kx. The work done by the spring is
Wsp=−12kx2
The work done by gravity is Wgr=mgx
The block does not change its kinetic energy as it is lowered slowly, ΔK=0
Assuming Wext as the work done by the applied external force by applying work-energy theorem, we have
Work done by total forces is equal to change in kinetic energy of the system.
W→tal=ΔK
Wext=Wsp+Wgr=ΔK
Substituting Wsp=−12kx2, Wgr=mgx, and ΔK=0, we
have Wext−12kx2+mgx=0
b. When the block remains at rest under the action of gravity and spring force, as the continuously increasing spring force kx will nullify the gravity force mg, we have kx=mg.
This gives x=mg/k which corresponds to stable euilibrium position. Now substituting x=mg/k in the expression,
Wext=12kx2−mgx, we have Wext=−m2g22k
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
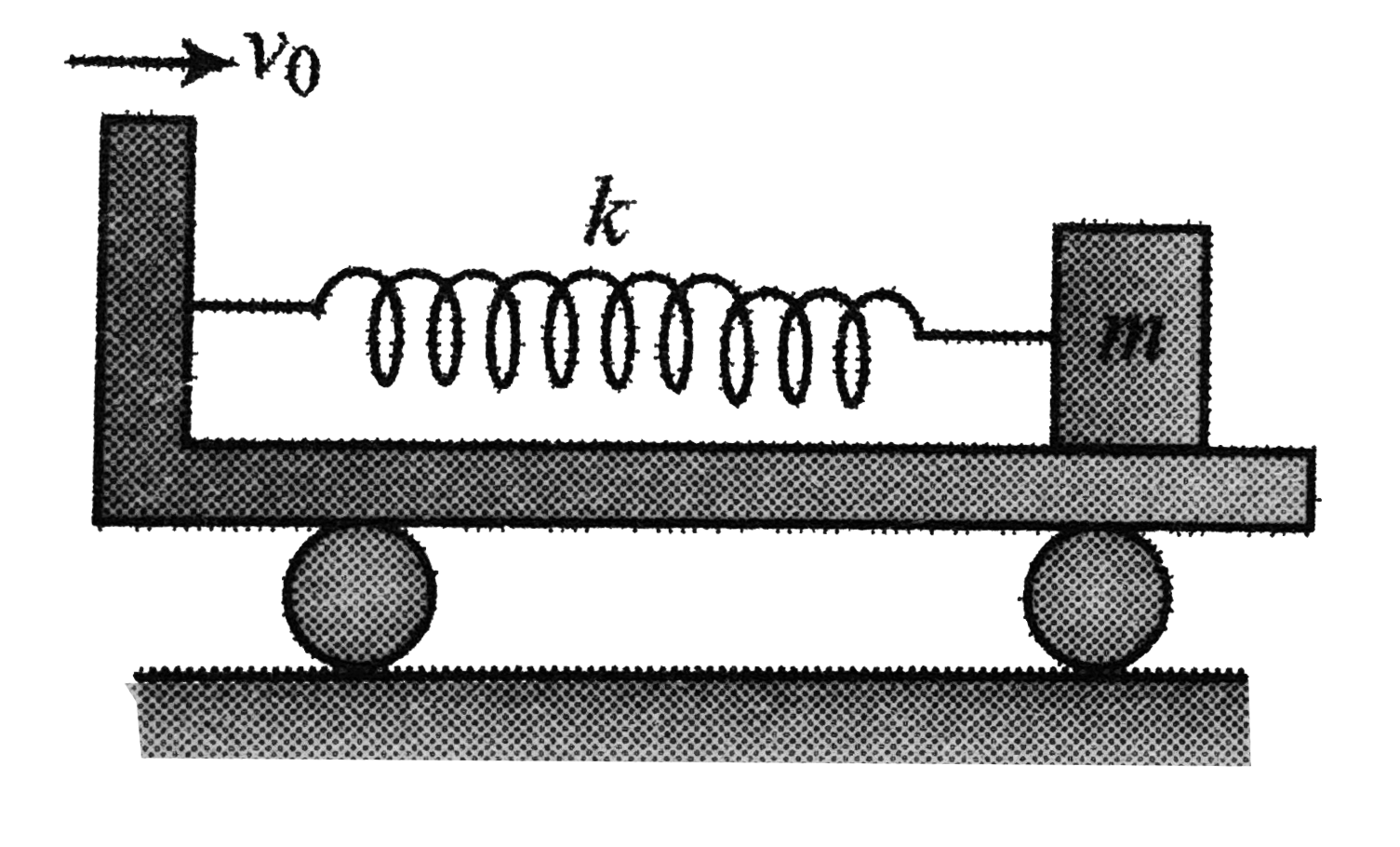
A block of mass m is connected rigidly with a smooth wedge (plank) by a light spring of stiffness k. If the wedge is moved with constant velocity v0, find the work done by the external agent till the maximum compression of the spring.
View SolutionFind the work done by an external agent in lowering a block of mass m slowly on a light of stiffness k, till it comes to rest.
View Solution
Knowledge Check
A body of mass m dropped from a certain height strikes a light vertical fixed spring of stifness k. the height of its fall before touching the spring the if the maximum compression of the spring the equal to 3mgk is
A3mg2kB2mgkC3mg4kDmg4k
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2
A block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
View SolutionA block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA spring of spring constasnt 50 N/m is compressed from its natural position through 1 cm. Find the work done by the work done by the spring force on the agency compressing the spring.
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

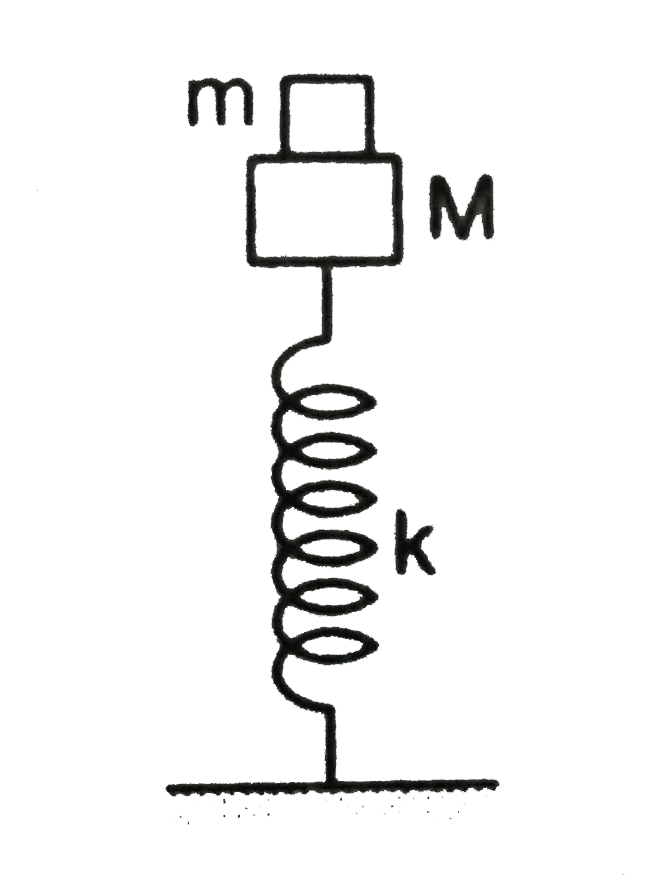
View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.

a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View Solution
