A block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
To solve the problem of how far below the equilibrium position the block comes to an instantaneous rest after being given an initial downward velocity v, we can follow these steps:
Step 1: Understand the forces acting on the block
When the block is in equilibrium, the downward gravitational force mg is balanced by the spring force kx, where x is the extension of the spring from its natural length.
Step 2: Determine the equilibrium position
At equilibrium, we have:
mg=kx
From this, we can express x as:
x=mgk
Step 3: Analyze the situation after the blow
After the block receives a sharp blow, it has an initial downward velocity v. As it moves downward, the spring stretches further, and the kinetic energy of the block will be converted into potential energy of the spring and the gravitational potential energy.
Step 4: Set up the energy conservation equation
We will use the principle of conservation of energy. The total mechanical energy at position 1 (just after the blow) will equal the total mechanical energy at position 2 (when the block comes to rest).
At position 1:
- Kinetic Energy (KE) = 12mv2
- Potential Energy (PE) of the spring = 12kx2
Total energy at position 1:
E1=12mv2+12kx2
At position 2 (where the block comes to rest):
- The spring is extended by an additional distance δx, so the new extension is x+δx.
- The potential energy of the spring becomes 12k(x+δx)2.
- The gravitational potential energy lost by the block as it moves down δx is mgδx.
Total energy at position 2:
E2=12k(x+δx)2−mgδx
Step 5: Set the energies equal
Using conservation of energy:
E1=E2
Substituting the expressions for E1 and E2:
12mv2+12kx2=12k(x+δx)2−mgδx
Step 6: Expand and simplify the equation
Expanding 12k(x+δx)2:
12k(x2+2xδx+δx2)−mgδx
This gives:
12mv2+12kx2=12kx2+kxδx+12kδx2−mgδx
Step 7: Cancel and rearrange terms
Cancel 12kx2 from both sides:
12mv2=kxδx+12kδx2−mgδx
Step 8: Rearranging to isolate δx
Rearranging gives:
12mv2+mgδx=kxδx+12kδx2
This is a quadratic equation in δx.
Step 9: Solve for δx
To solve for δx, we can rearrange it into standard quadratic form:
12kδx2+(kx−mg)δx−12mv2=0
Using the quadratic formula:
δx=−b±√b2−4ac2a
where a=12k, b=kx−mg, and c=−12mv2.
Step 10: Final expression for δx
After solving, we find:
δx=√mv2k
Conclusion
The block comes to an instantaneous rest at a distance δx=v√m√k below the equilibrium position.
---
When the block is in equilibrium, the downward gravitational force mg is balanced by the spring force kx, where x is the extension of the spring from its natural length.
At equilibrium, we have:
mg=kx
From this, we can express x as:
x=mgk
After the block receives a sharp blow, it has an initial downward velocity v. As it moves downward, the spring stretches further, and the kinetic energy of the block will be converted into potential energy of the spring and the gravitational potential energy.
We will use the principle of conservation of energy. The total mechanical energy at position 1 (just after the blow) will equal the total mechanical energy at position 2 (when the block comes to rest).
- Kinetic Energy (KE) = 12mv2
- Potential Energy (PE) of the spring = 12kx2
E1=12mv2+12kx2
- The spring is extended by an additional distance δx, so the new extension is x+δx.
- The potential energy of the spring becomes 12k(x+δx)2.
- The gravitational potential energy lost by the block as it moves down δx is mgδx.
E2=12k(x+δx)2−mgδx
Using conservation of energy:
E1=E2
Substituting the expressions for E1 and E2:
12mv2+12kx2=12k(x+δx)2−mgδx
Expanding 12k(x+δx)2:
12k(x2+2xδx+δx2)−mgδx
This gives:
12mv2+12kx2=12kx2+kxδx+12kδx2−mgδx
Cancel 12kx2 from both sides:
12mv2=kxδx+12kδx2−mgδx
Rearranging gives:
12mv2+mgδx=kxδx+12kδx2
This is a quadratic equation in δx.
To solve for δx, we can rearrange it into standard quadratic form:
12kδx2+(kx−mg)δx−12mv2=0
Using the quadratic formula:
δx=−b±√b2−4ac2a
where a=12k, b=kx−mg, and c=−12mv2.
After solving, we find:
δx=√mv2k
The block comes to an instantaneous rest at a distance δx=v√m√k below the equilibrium position.
Topper's Solved these Questions
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Worked out Examples
14 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -1
10 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View Solution
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. Find the time taken by the block to cross the mean position for the first time.
View Solution
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. Find the amplitude.
View Solution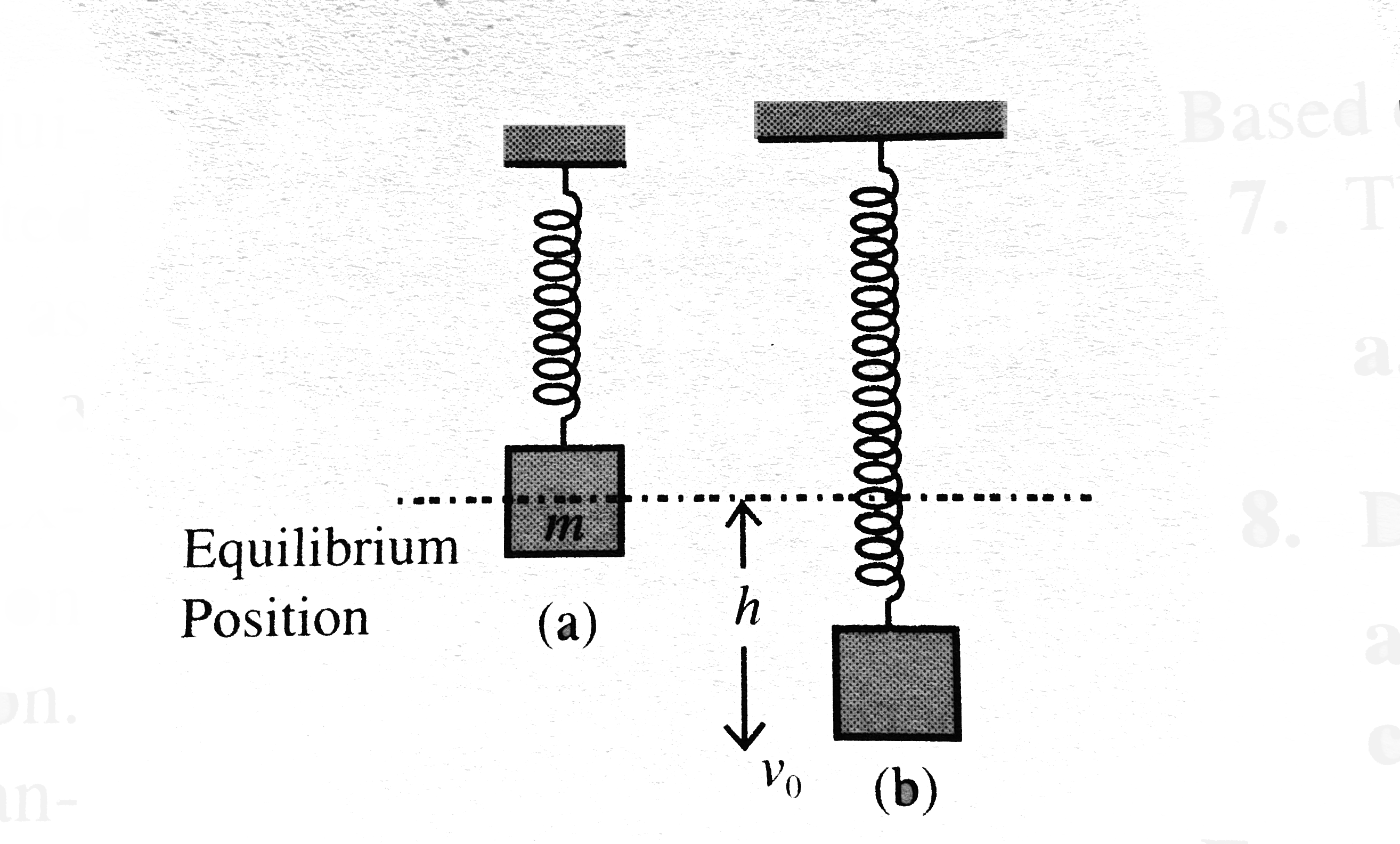
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The amplitude of oscillation is
View Solution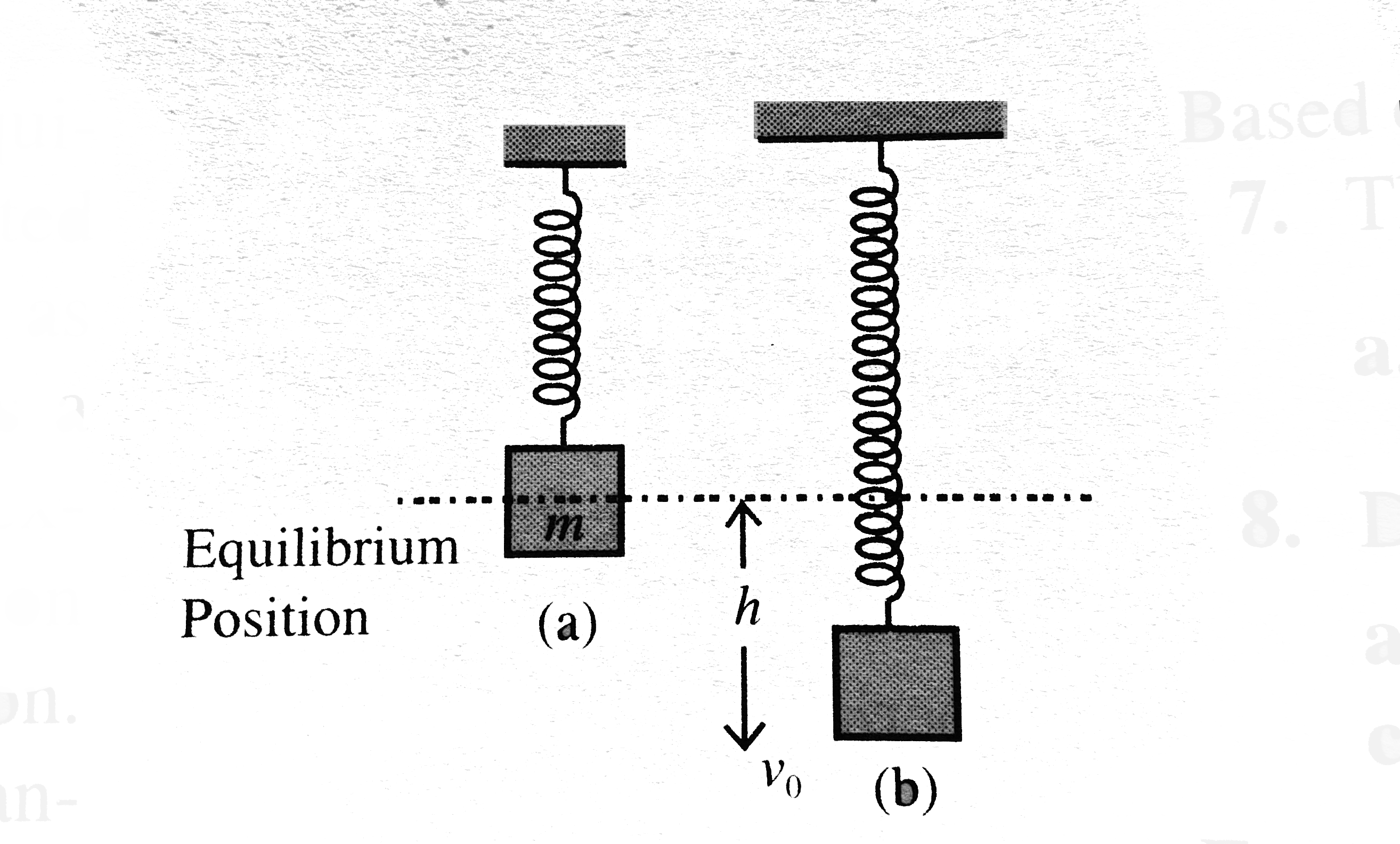
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The equation for the simple harmonic motion is
View Solution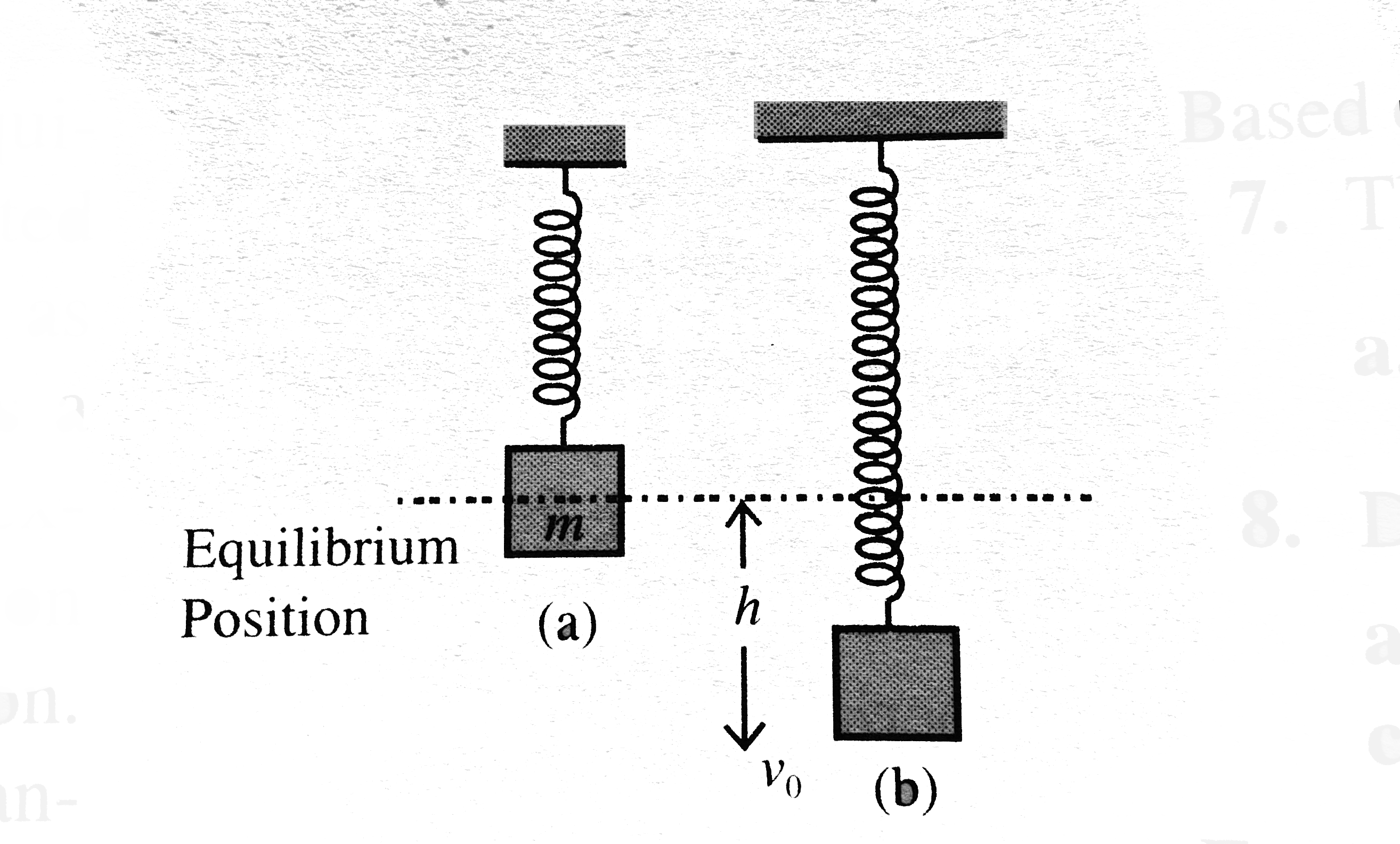
A block of mass m is connected to a spring constant k and is at rest in equilibrium as shown. Now, the block is Displacement by h below its equilibrium position and imparted a speed v0 towards down as shown in the Fig. As a result of the jerk, the block executes simple harmonic motion about its equilibrium position. Based on this information, answer the following question.
Q. The equation for the simple harmonic motion is
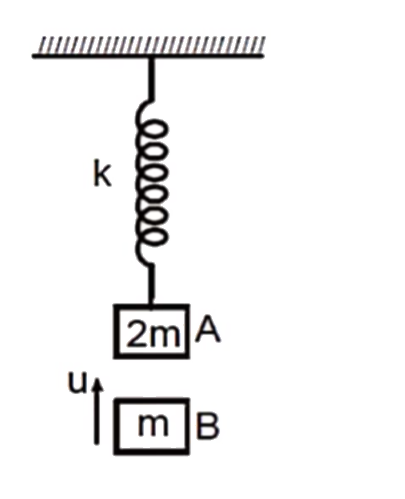
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass 'm' is hanging from a massless spring of spring constant K. It is in equilibrium under the influence of gravitational force. Another particle of same mass 'm' moving upwards with velocity ao hits the block and sticks to it. For the subsequent motion, choose the incorrect statements:

View Solution
