A block of mass m is suspened through a spring of spring constant k and is in equlibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium psitin, the block comes to an instantaneous rest?
Klet us consider the blockthe spring+the earth as the system. The system has gravitatioN/Al potential energy corresponding to the force between the block and the earth as well as the elastic potential energy corresponding to the sring force. The total mechanicla energy includes kinetic enegy, gravitatioN/Al potential energy and elastic potential energy.
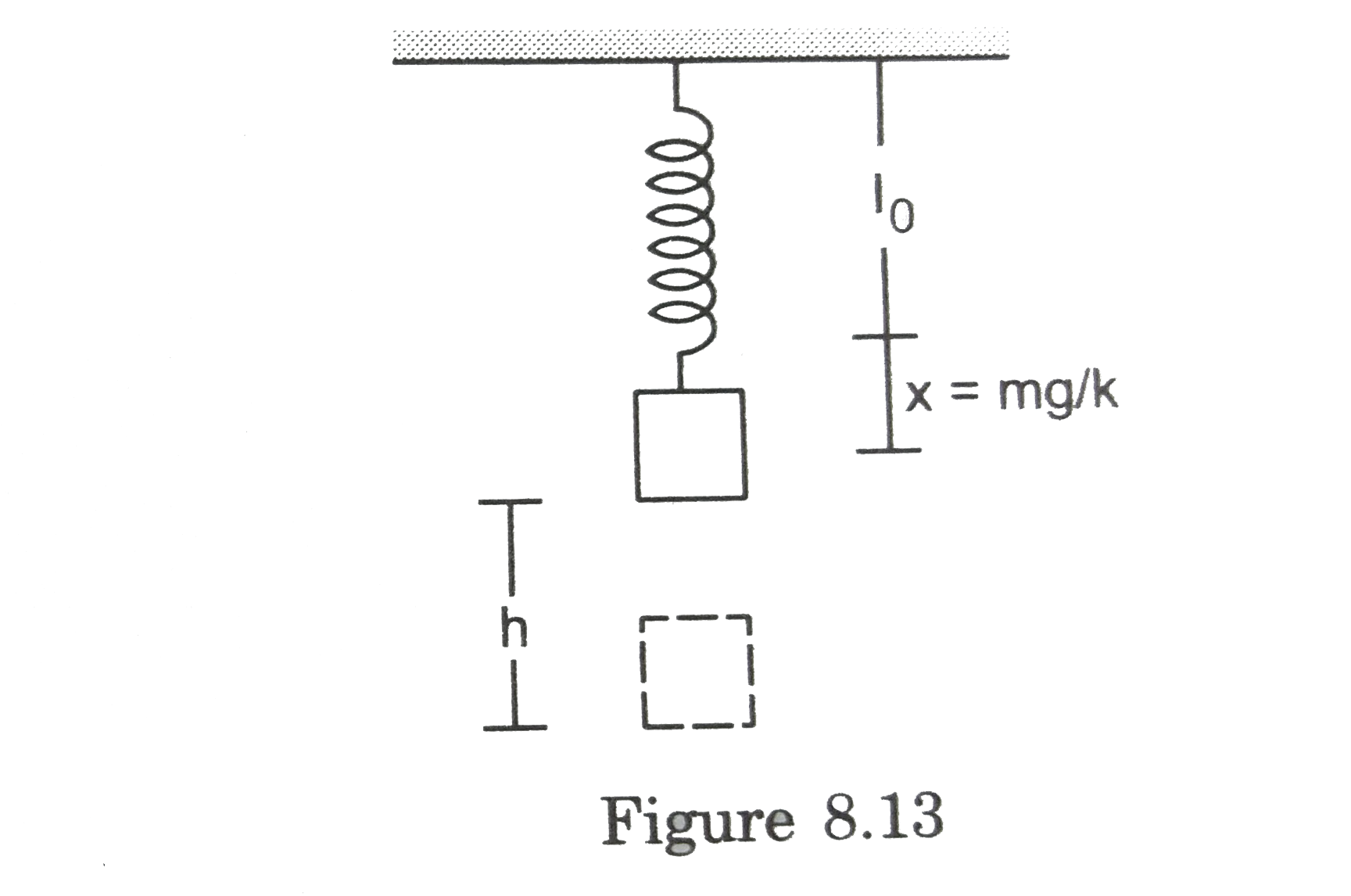
When the block is in equilibrium it is acted upon by two forces, a. the force of gravity mg and b. the tension in the spring T−kx. where x is the elongation. For equilibrium, mg=kx, so that the spring is stretched by a length x=mgk.Thepotentiale≠rgyofthespr∈g∈thispositionis<br>1/2 k(mg/k)^2=(m^2g^2)/(2k)<br>TakethegravitatioNAlpotentiale≠rgy→bezero∈thisposition..The→talmechaniclae≠rgyofthesystemjustaftertheblowis<br>1/2 mv^2+(m^2g^2)/(2k)<br>TheonlyexterNAlforceonthissystemistˆdue→the⌈∈⌉gwhichdoesnowork.Hence,themechanicale≠rgyothissystemrema∈sconstant.Iftheblockdescendsthroughaheighthbeforecomingbecomes<br>1/2k9mg/k+h)^2andthegravitatioNAlpotentiale≠rgy−mgh.thek∈etice≠rgyiszeroisthisstate.Thuswehave<br>1/2mv^2+(m^2g^2)/(2k)=1/2k(mg/k+h)^2-mgh<br>Solv∈gthiswe≥t,<br>h=vsqrt(m/k)
Compare this with the result obtained in example. If we neglect gravity and consider the length of the spring in equilibrium position as the N/Atural length, the answer is same. This simplication is often used while dealing with vertical springs.
Topper's Solved these Questions
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
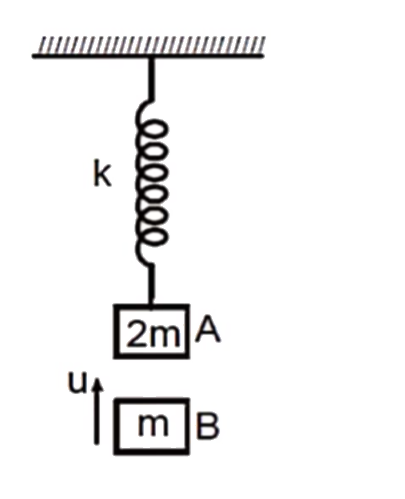
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k - Question 2 - Select One
Two block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
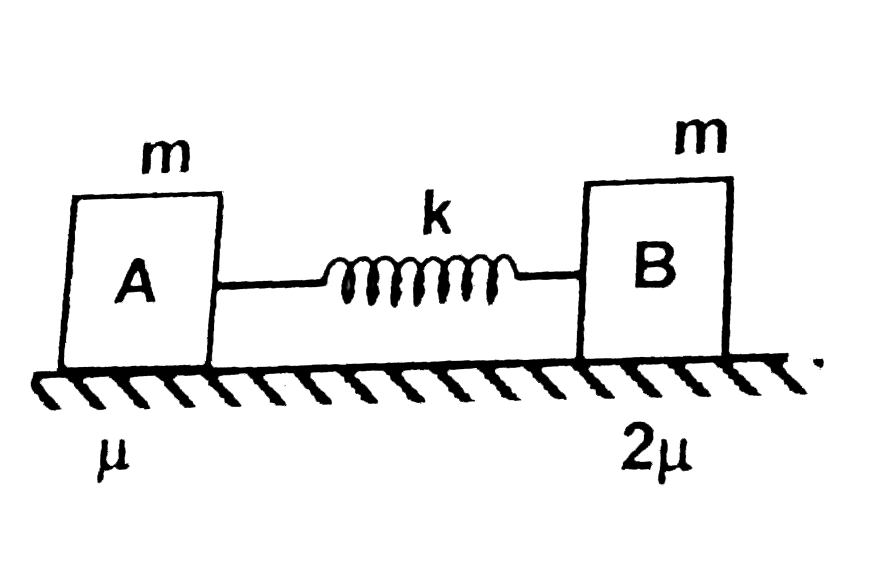 A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
A2μg√2mkBμg√2mkCμg√mkD2μg√m2k - Question 3 - Select One
A block of mass m=0.1kg is connceted to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the euilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
A0.6 JB0.8 JC1.5 JD0.3 J
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionConsider the spring blcok system shoen in the figure initially block m is in equlibrium. An impulse gives the block a velocity v upwards. Find the maximum speed of the block during the motion.
 View Solution
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :
 View Solution
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :
 View Solution
View Solution

