A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

Fπ√mk
πF√mk
F√mk
2F√mk
The correct Answer is:D
For maximum velocity , a = 0
⇒x=Fk …(i)
Apply work energy theorem

Wspring+WF=ΔK.E
−12kx2+Fx=ΔK.E
−12kF2k2+F2k=(12mv2max−12m(0)2)
F22k=12mv2max⇒vmax=F√mk
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (JEE (Advanced) for IIT Entrance)
7 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (C. Multiple Choice Questions)
16 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (B. Multiple Choice Questions)
46 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
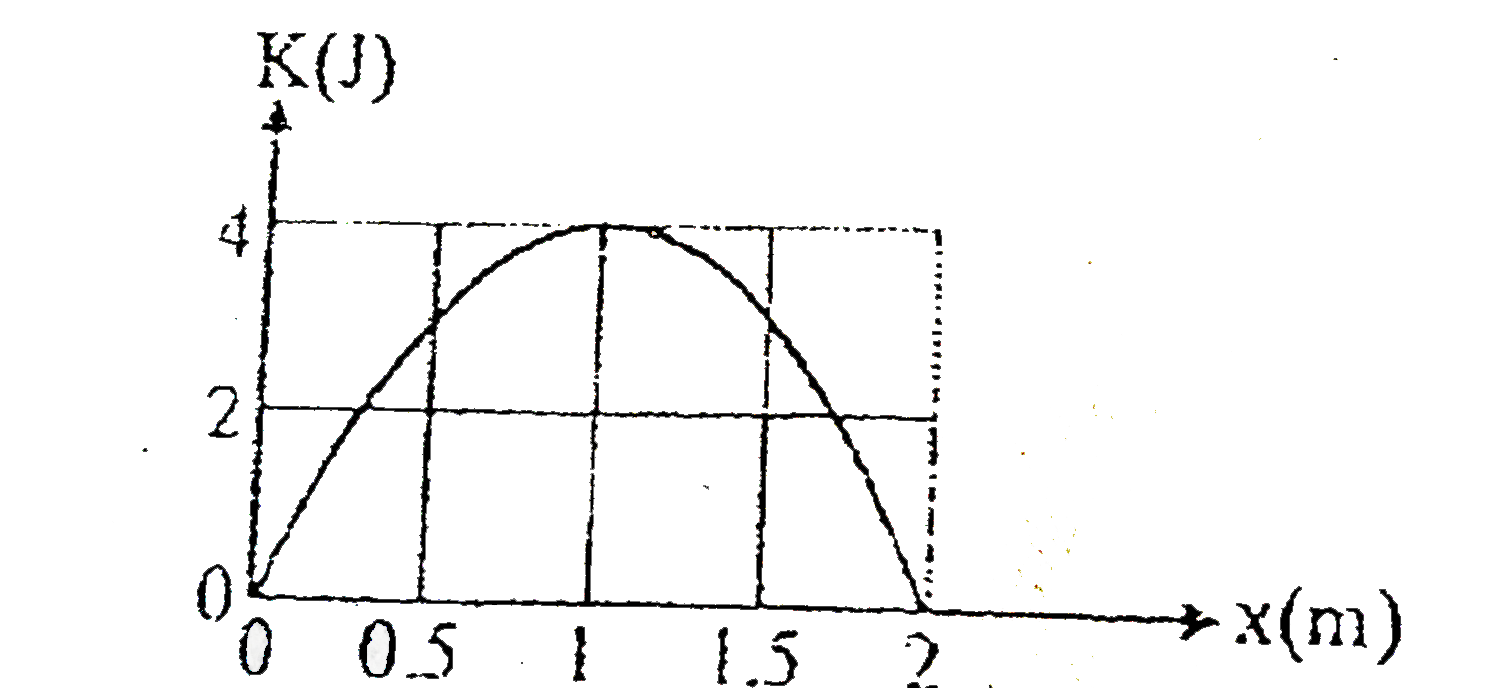 A2NB4NC8ND16N
A2NB4NC8ND16NA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a costant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block verus its position x is shown in figure. What is the magnitude of →F
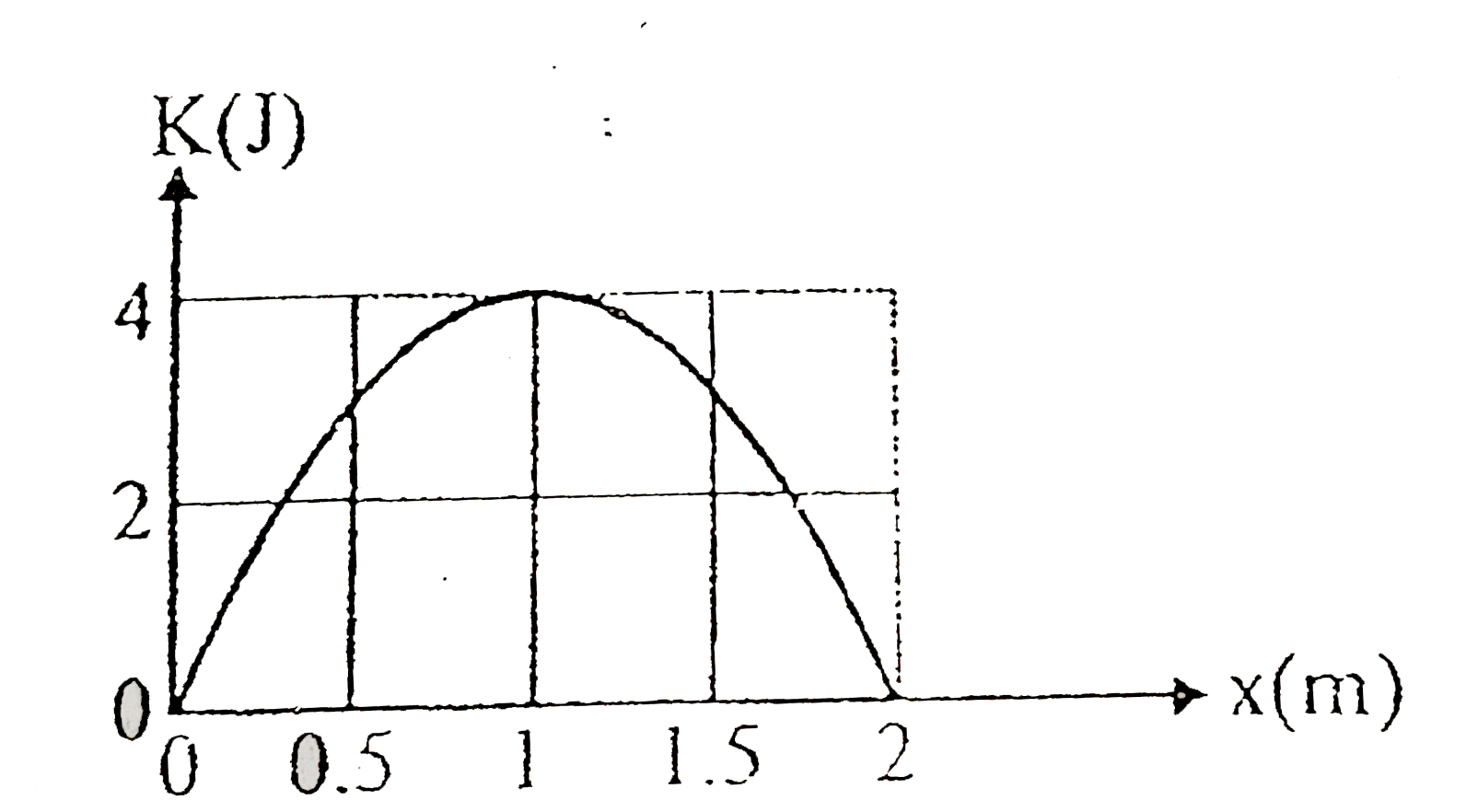 A2NB4NC8ND16N
A2NB4NC8ND16N
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
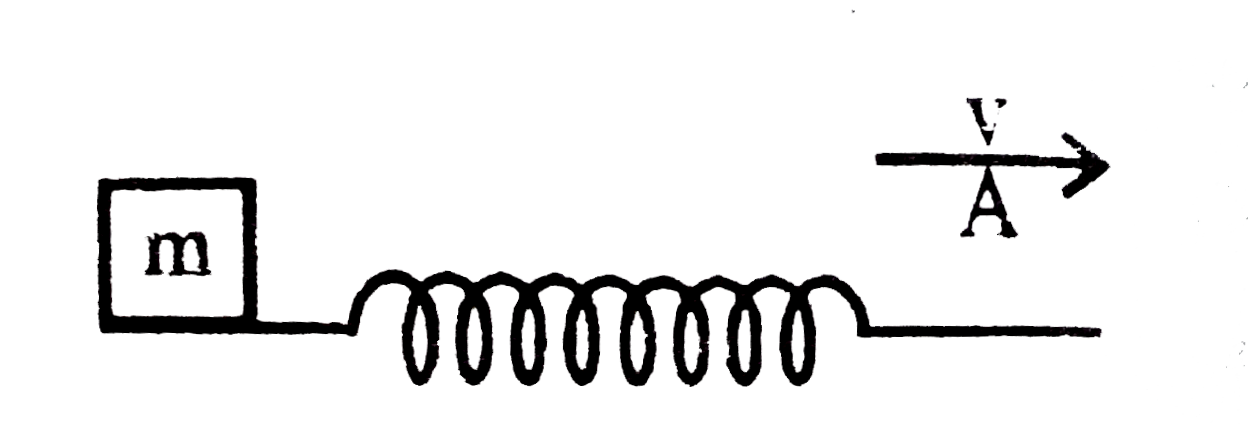
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
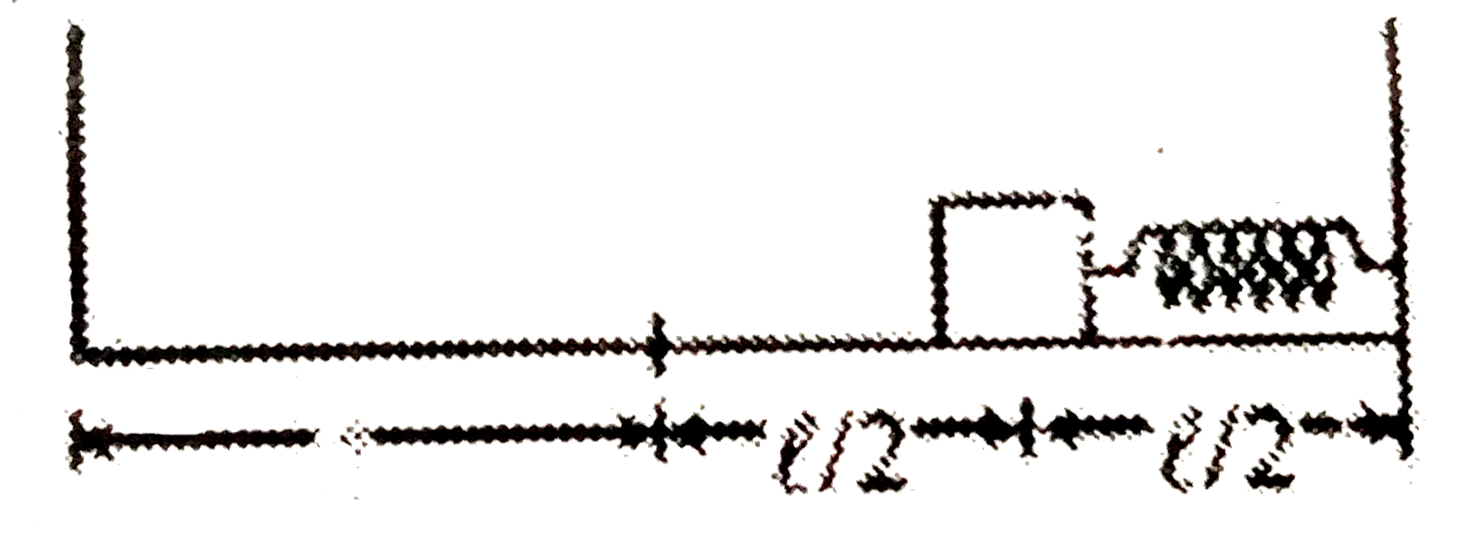
View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in the figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truj starts moving towards right with a constant acceleration a0. If the block is observed from the truck
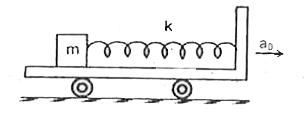
View SolutionA block of mass m is placed on a smooth horizontal floor is attached to one end of spring. The other end of the spring is attached to fixed support. When spring is vertical it is relaxed. Now the block is pulled to wards right by a force F, which is being increased gradually. When the speing makes angle 53∘ with the vertical, block leaves the floor.

Force constant of the spring is :-
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution
