A block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
12
1
13
14
The correct Answer is:A
From conservation of linear momentum, we can see that velocity of 2m will become v/2 after collision (as mass is doubled)
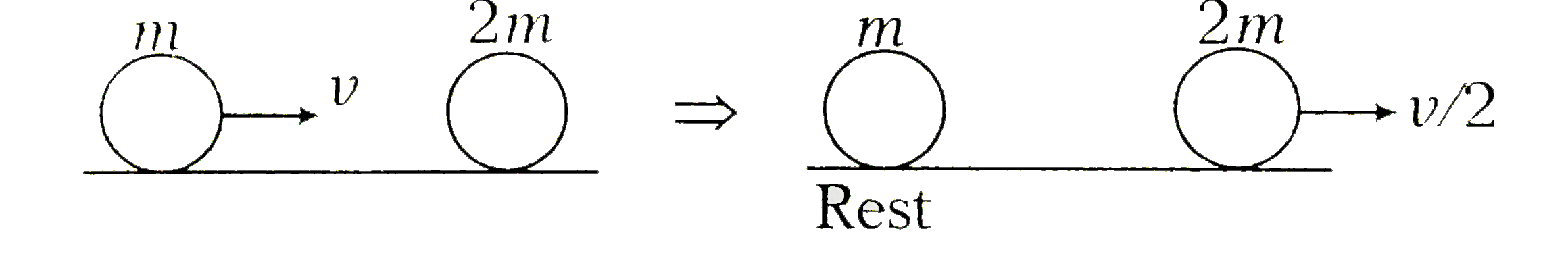
Now, e = (Relative velocity of separation)/(Relative velocity of approach) = (v/2)/(v) = 1/2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View SolutionA block of mass m moving at a velocity υ collides head on with another block of mass 2m at rest. If the coefficient of restitution is 1/2, find the velocities of the blocks after the collision.
View SolutionA block of mass m moving at speed υ collides with another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionAn object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.
View SolutionAn object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.
View SolutionBody A of mass 4m moving with speed u collides with another body B of mass 2m at rest the collision is head on and elastic in nature. After the collision the fraction of energy lost by colliding body A is :
View Solution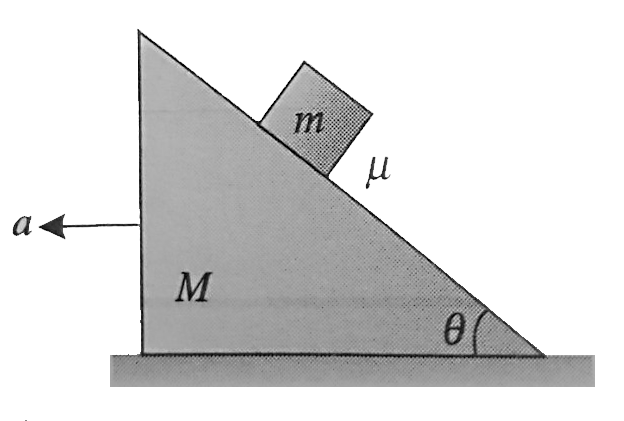
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionA moving block having mass m , collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the block is v, then the value of coefficient of restitution (e) will be
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View Solution
