Doubtnut Promotions Sticky

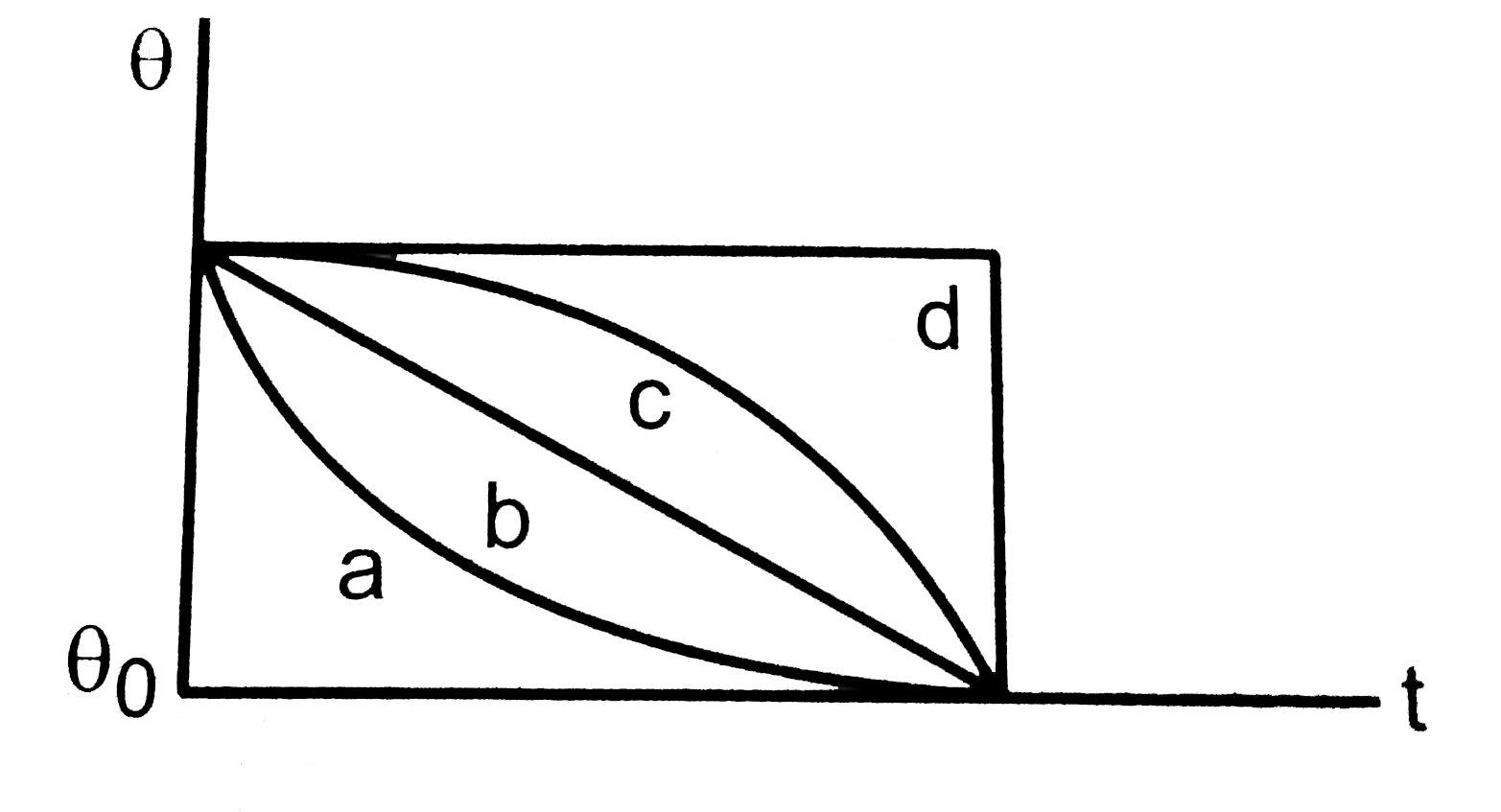
A block of metal is heated to a temperature much higher than the room temperature and allowed to cool in a room free from air currents. Which of the following curves correctly represents the rate of cooling

A

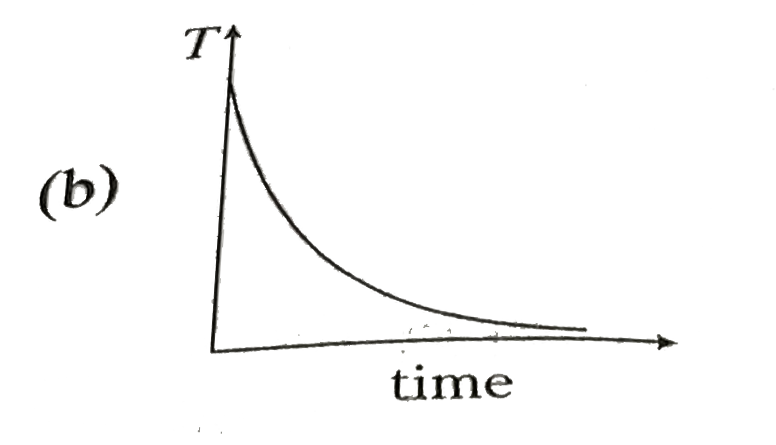
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem of determining the correct curve that represents the rate of cooling of a heated metal block, we can follow these steps:

Step 1: Understand Newton's Law of Cooling
Newton's Law of Cooling states that the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature. Mathematically, this can be expressed as:

dTdt=−k(T−T0)

where:
- T is the temperature of the object,
- T0 is the ambient temperature,
- k is a positive constant that depends on the characteristics of the object and the environment.

Step 2: Set Up the Initial Conditions
Assume the initial temperature of the metal block is Ti (much higher than T0), and we want to find the temperature Tf at time t.

Step 3: Integrate the Equation
We can rearrange the equation and integrate it:

∫dTT−T0=−k∫dt

This results in:

ln|T−T0|=−kt+C

where C is the integration constant.

Step 4: Solve for the Constant
To find C, we can use the initial condition at t=0:

ln|Ti−T0|=C

Step 5: Substitute Back
Substituting back into the equation gives:

ln|T−T0|=−kt+ln|Ti−T0|

Exponentiating both sides results in:

|T−T0|=|Ti−T0|e−kt

Step 6: Final Temperature Equation
This can be simplified to:

T=T0+(Ti−T0)e−kt

This shows that the temperature T approaches T0 as t increases, and the rate of cooling is exponential.

Step 7: Analyze the Graphs
From the derived equation, we can see that the temperature decreases exponentially over time. Therefore, we need to identify which of the given curves represents an exponential decay.

Step 8: Conclusion
After analyzing the options, we find that:

- Option B represents an exponential decrease in temperature over time, which matches our derived equation.
- Other options either show linear decrease or do not approach the ambient temperature correctly.

Thus, the correct answer is Option B.

---

|
Updated on:7/8/2024
Class 11PHYSICSTHERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

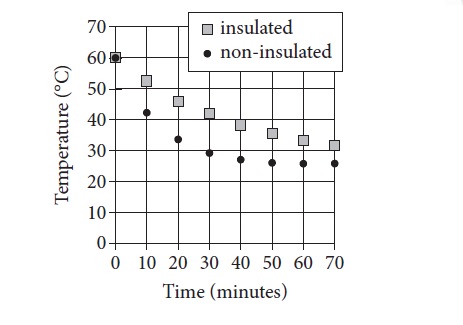
    ocr_image
    Two samples of water of equal mass are heated to 60 degrees Celsius (°C). One sample is poured into an insulated container, and the other sample is poured into a non-insulated container. The samples are then left for 70 minutes to cool in a room having a temperature of 25°C. The graph above shows the temperature of each sample at 10-minute intervals. Which of the following statements correctly compares the average rates at which the temperatures of the two samples change?

    AIn every 10-minute interval, the magnitude of the rate of change of temperature of the insulated sample is greater than that of the non-insulated sample.
    BIn every 10-minute interval, the magnitude of the rate of change of temperature of the non-insulated sample is greater than that of the insulated sample.
    CIn the intervals from 0 to 10 minutes and from 10 to 20 minutes, the rates of change of temperature of the insulated sample are of greater magnitude, whereas in the intervals from 40 to 50 minutes and from 50 to 60 minutes, the rates of change of temperature of the non-insulated sample are of greater magnitude.
    DIn the intervals from 0 to 10 minutes and from 10 to 20 minutes, the rates of change of temperature of the non-insulated sample are of greater magnitude, whereas in the intervals from 40 to 50 minutes and from 50 to 60 minutes, the rates of change of temperature of the insulated sample are of greater magnitude.