A block with a mass of 3.00kg is suspended from an ideal spring having negligible mass and stretches the spring by 0.2m.
(a) What is the force constant of the spring?
(b) What is the period of oscillation of the block if it is pulled down and released ?
(i) In equlibrium , kl=mg∴k=mgl
Substituting the proper values, we have
k=(3)(9.8)0.2=147Nm−1
(ii) T=2π√lg=2π√0.29.8=0.897s
Similar Questions
When a mass of 5 kg is suspended from a spring of negligible mass and spring constant K, it oscillates with a periodic time 2π. If the mass is removed, the length of the spring will decrease by
View SolutionA mass M is suspended from a massless spring. An additional mass m stretches the spring further by a distance x. The combined mass will oscillate with a period
View SolutionA mass M is suspended from a massless spring. An additional mass m stretches the spring further by a distance x. The combined mass will oscillate with a period
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
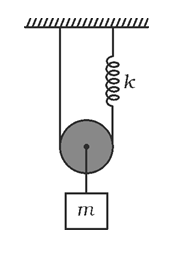 View Solution
View SolutionA block of 2 kg is suspended from the ceiling through a massless spring of spring constant k=100 N/m. What is the elongation of the spring? If another 1 kg is added to the block, what would be the further elongation?
View SolutionA spring mass system has time period of 2 second. What should be the spring constant of spring if the mass of the block is 10grams ?
View SolutionA force of 6.4 N stretches a vertical spring by 0.1 m. The mass (in kg) that must be suspended from the spring so that it oscillates with a time period of π4 second.
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionIn the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.
 View Solution
View Solution

