A block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.
To solve the problem step by step, we will break it down into two parts as requested:
Part (a): Putty Dropped at Equilibrium Position
1. Initial Conditions:
- The mass of the block is M.
- The spring constant is k.
- The initial amplitude of the block's motion is A1.
- The putty mass is m.
2. Velocity at Equilibrium Position:
- At the equilibrium position, the potential energy stored in the spring is converted into kinetic energy.
- The potential energy when the block is at amplitude A1 is given by:
PE=12kA21
- The kinetic energy (KE) when the block passes through the equilibrium position is:
KE=12(M)v20
- Setting PE=KE:
12kA21=12Mv20
- From this, we can solve for v0:
v0=√kA21M
3. After the Putty Sticks:
- When the putty sticks to the block, the new mass becomes (M+m).
- The momentum before and after the collision must be conserved:
Mv0=(M+m)v′
- Solving for v′:
v′=Mv0M+m
4. New Amplitude:
- The new amplitude A2 can be found using the conservation of energy:
12(M+m)v′2=12kA22
- Substituting v′:
12(M+m)(Mv0M+m)2=12kA22
- Simplifying gives:
M2v20M+m=kA22
- Using v20=kA21M:
M2kA21MM+m=kA22
- Thus:
A22=MA21M+m
- Therefore:
A2=A1√MM+m
5. New Period:
- The new period T′ is given by:
T′=2π√M+mk
Part (b): Putty Dropped at One End of the Path
1. Initial Conditions:
- The block is at one end of its path, so its velocity is zero at that point.
2. Kinetic Energy:
- When the putty drops onto the block at the maximum amplitude, the initial kinetic energy is zero.
3. Momentum Conservation:
- Since the block is momentarily at rest, the momentum conservation gives:
0=(M+m)v′
- Thus, the new velocity v′ is still zero.
4. New Amplitude:
- Since the block is at rest, we can use the potential energy at maximum amplitude:
12kA21=12(M+m)v′2
- Since v′=0, the energy is conserved, and the amplitude does not change:
A2=A1
5. New Period:
- The period remains the same as the mass of the system has not changed:
T′=2π√M+mk
Final Answers:
- (a) New Amplitude: A2=A1√MM+m, New Period: T′=2π√M+mk
- (b) New Amplitude: A2=A1, New Period: T′=2π√M+mk
- The mass of the block is M.
- The spring constant is k.
- The initial amplitude of the block's motion is A1.
- The putty mass is m.
- At the equilibrium position, the potential energy stored in the spring is converted into kinetic energy.
- The potential energy when the block is at amplitude A1 is given by:
PE=12kA21
- The kinetic energy (KE) when the block passes through the equilibrium position is:
KE=12(M)v20
- Setting PE=KE:
12kA21=12Mv20
- From this, we can solve for v0:
v0=√kA21M
- When the putty sticks to the block, the new mass becomes (M+m).
- The momentum before and after the collision must be conserved:
Mv0=(M+m)v′
- Solving for v′:
v′=Mv0M+m
- The new amplitude A2 can be found using the conservation of energy:
12(M+m)v′2=12kA22
- Substituting v′:
12(M+m)(Mv0M+m)2=12kA22
- Simplifying gives:
M2v20M+m=kA22
- Using v20=kA21M:
M2kA21MM+m=kA22
- Thus:
A22=MA21M+m
- Therefore:
A2=A1√MM+m
- The new period T′ is given by:
T′=2π√M+mk
- The block is at one end of its path, so its velocity is zero at that point.
- When the putty drops onto the block at the maximum amplitude, the initial kinetic energy is zero.
- Since the block is momentarily at rest, the momentum conservation gives:
0=(M+m)v′
- Thus, the new velocity v′ is still zero.
- Since the block is at rest, we can use the potential energy at maximum amplitude:
12kA21=12(M+m)v′2
- Since v′=0, the energy is conserved, and the amplitude does not change:
A2=A1
- The period remains the same as the mass of the system has not changed:
T′=2π√M+mk
- (a) New Amplitude: A2=A1√MM+m, New Period: T′=2π√M+mk
- (b) New Amplitude: A2=A1, New Period: T′=2π√M+mk
Similar Questions
A particle performs simple harmonic motion wit amplitude A. its speed is double at the instant when it is at distance A3 from equilibrium position. The new amplitude of the motion is
View SolutionA horizontal spring block system of mass M executes simple harmonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
View SolutionA horizontal spring -block system of mass 2kg executes S.H.M when the block is passing through its equilibrium position an object of mass 1kg is put on it the two move together The new amplitude of vibration is (A being its initial amplitude)
View SolutionA horizontal spring -block system of mass 2kg executes S.H.M when the block is passing through its equilibrium position an object of mass 1kg is put on it the two move together The new amplitude of vibration is (A being its initial amplitude)
View SolutionA mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?

View SolutionA block of mass M attached to the free end of a spring of force constant k is nounted on a smooth horizontal table as shown in figure.
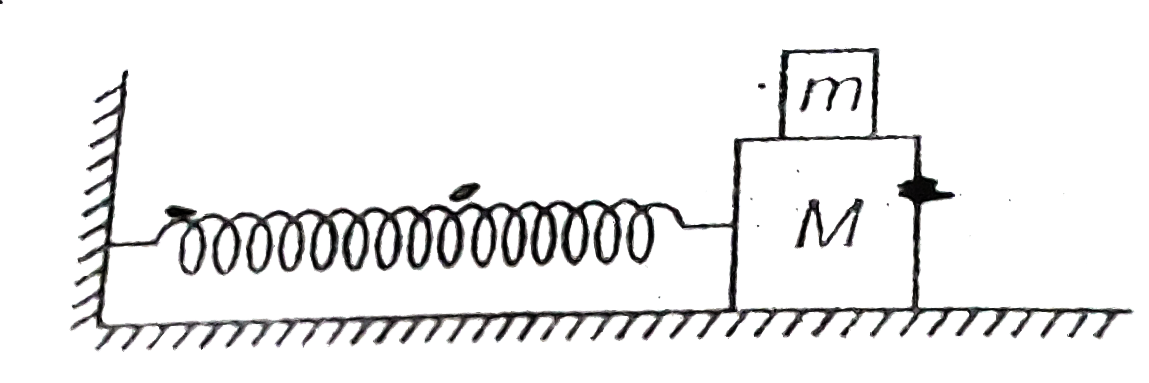
The block executes SHM with amplitude A and frequency f . If an object of mass m is put on it, when the block is passing through its equilibium position and the two move together ,then what is the new amplitude and frequency of vibration?
View SolutionA particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance
2A3 from equilibrium position. The new amplitude of the motion is:
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA particle performs simple harmonic motion with amplitude A. its speed is double at the instant when it is at distance A3 from equilibrium position. The new amplitude of the motion is √33Aβ. Find β
View SolutionA mass M, attached to a horizontal spring, excutes SHM with a amplitude A1. When the mass M passes through its mean position then a smaller mass m is placed over it and both of them move together with amplitude A2, the ratio of (A1A2) is :
View Solution