A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
1
3
5
1/5
The correct Answer is:C
Velocity of the first bob at A = √5gl1
Velocity of the first bob at B=√gl1
At point B it collides elastically with another bob of same mass m suspended by a string of length l2 as shown in figure.
When two bodies of equal masses undergoes an elastic collision, their velocities are interchanged.
∴ Velocity of the second bob at B=√gl1
But to complete the vertical circle, the velocity of the second bob at B = √5gl2
∴√gl1=√5gl2 or l1l2=5

Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT Exemplar
18 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason
15 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - Collisions
15 Videos
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The minimum velocity required to complete a full circle in a vertical plane is given to a bob of mass m suspended by a string of length 25 cm. When it reaches the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. After the collision, if the second bob acquires the minimum speed required to complete a full circle in the vertical plane, then the length of the string l2 __m. (Both the strings are massless and in-extensible)
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure. What will be X the trajectory of the particle if the string is cut at
(a) Point B
(b) Point C
(c) Point X
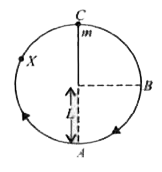
View Solution
Knowledge Check
A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elasticallywith another bob of mass 2m suspended by a string of length l2, which is initially at rest. Both strings are massless and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l2/l1 is (5/4)n. The value of n is
A3B6C9D5A particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCPeriod T=2π√lcosθgDCentripetal acceleration a=Fsinθm where F is tensionA body of mass m is suspended from a string of length l. What is minimum horizontal velocity that should be given to the body in its highest position so that it may complete one full revolution in the vertical plane with the point of suspension as the centre of the circle.
Av=√lgBv=√2lgCv=√4lgDv=√5lg
A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
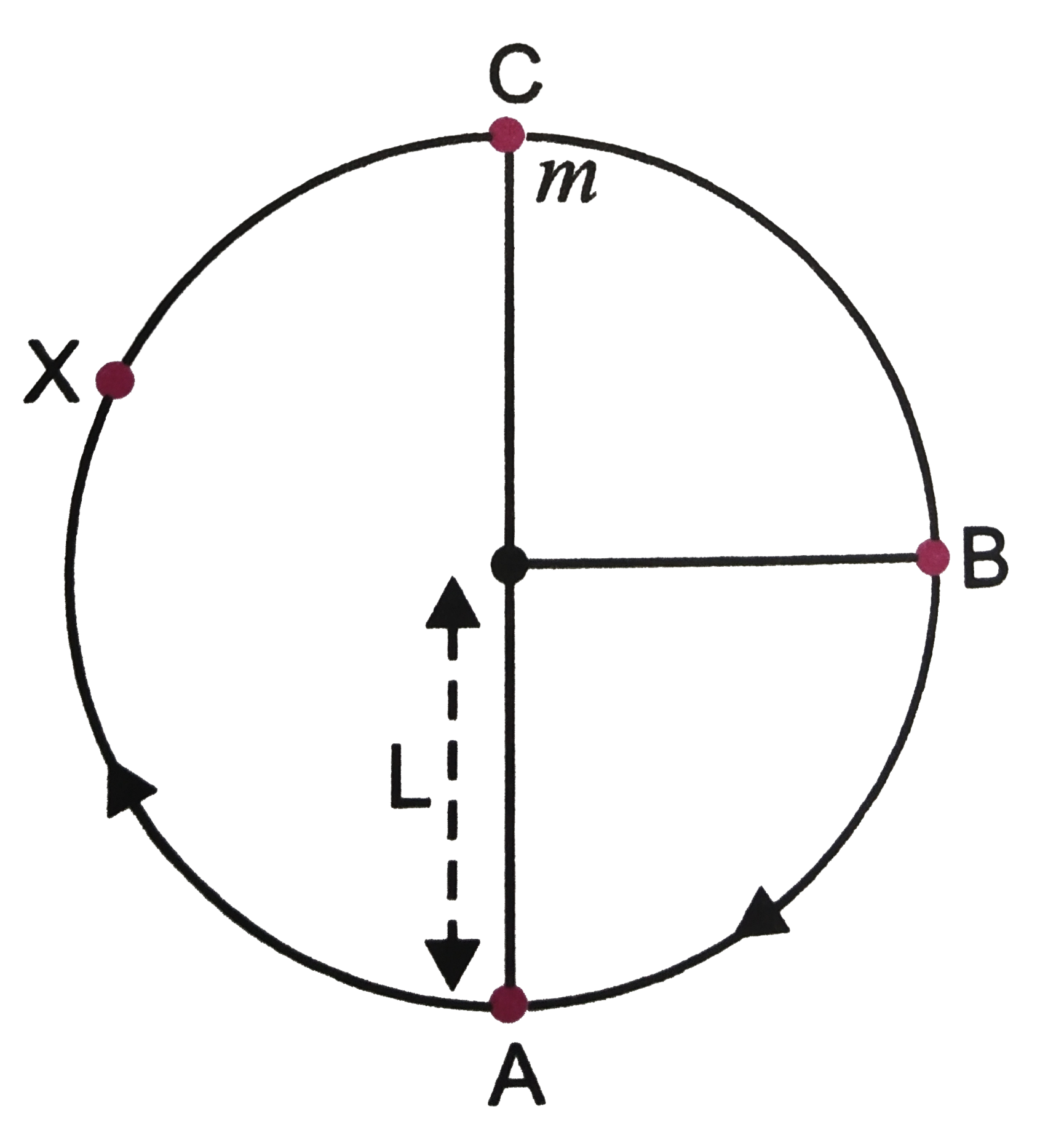
View SolutionA body of mass m is suspended from a string of length l . What is minimum horizontal velocity that should be given to the body in its lowest position so that it may complete one full revolution in the vertical plane with the point of suspension as the centre of the circle
View SolutionA bob of mas M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies.
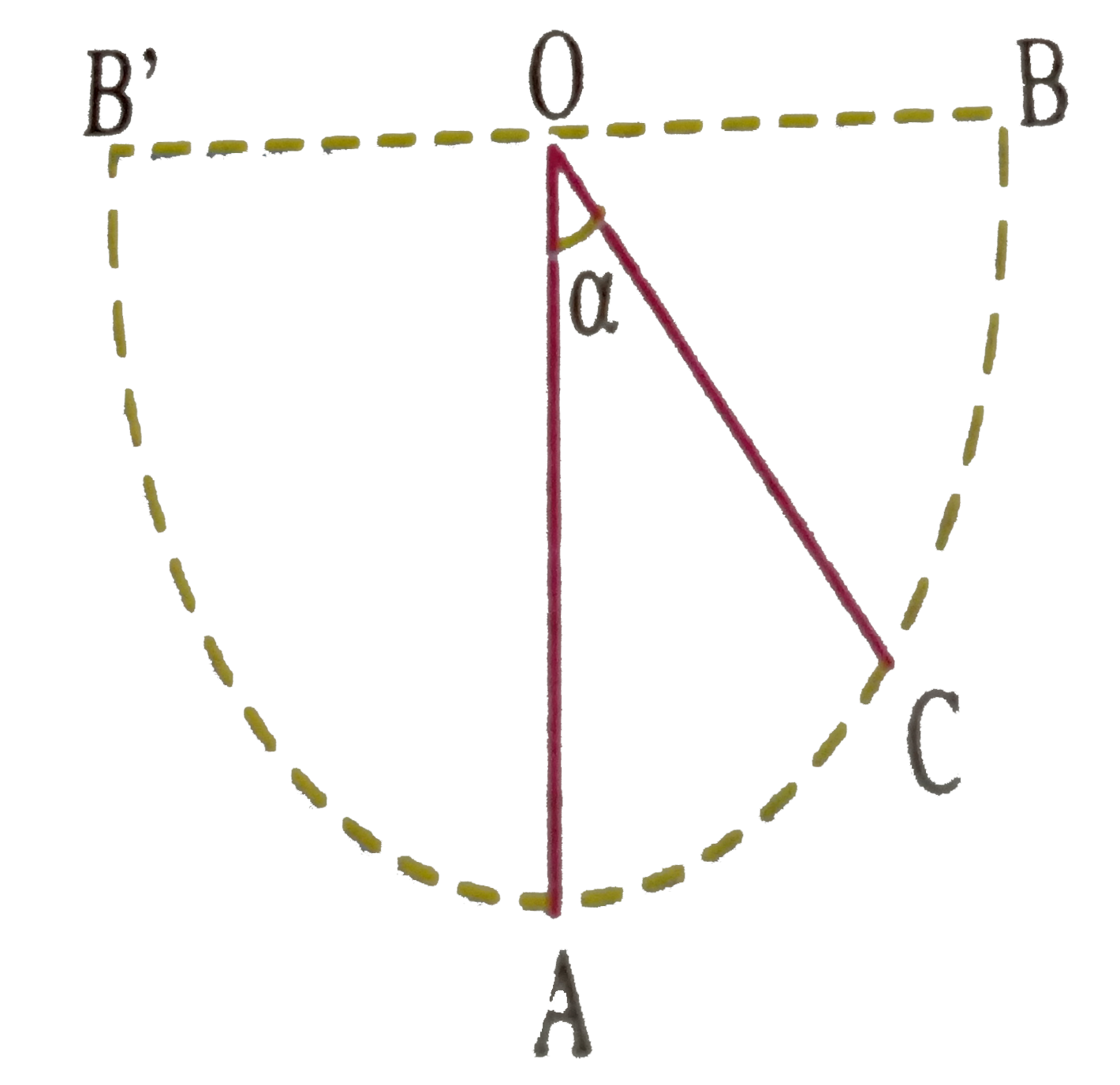 .
.
View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The vertical coordinate of the initial positon of the bob w.r.t. the point of firing of the bullet is
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View Solution
