A body covera in the seconds second and in finfth second of its motion. If the motion is uniformly accelerated, how farwill it go in the the seventh second?
To solve the problem of how far a body will travel in the seventh second of uniformly accelerated motion, we can use the equations of motion. Let's break it down step by step.
Step 1: Understand the formula for distance covered in the nth second
The distance covered in the nth second of uniformly accelerated motion can be calculated using the formula:
sn=u+a2(2n−1)
where:
- sn is the distance covered in the nth second,
- u is the initial velocity,
- a is the acceleration,
- n is the nth second.
Step 2: Set up equations for the second and fifth seconds
1. For the second second (n=2):
s2=u+a2(2⋅2−1)=u+a2⋅3
Given that s2=10m:
10=u+3a2(Equation 1)
2. For the fifth second (n=5):
s5=u+a2(2⋅5−1)=u+a2⋅9
Given that s5=25m:
25=u+9a2(Equation 2)
Step 3: Solve the system of equations
Now we have two equations:
1. 10=u+3a2
2. 25=u+9a2
Subtract Equation 1 from Equation 2 to eliminate u:
25−10=(u+9a2)−(u+3a2)
15=9a2−3a2
15=6a2
15=3a
a=5m/s2
Now substitute a back into Equation 1 to find u:
10=u+3⋅52
10=u+152
10=u+7.5
u=10−7.5=2.5m/s
Step 4: Calculate the distance covered in the seventh second
Now that we have u=2.5m/s and a=5m/s2, we can find the distance covered in the seventh second (n=7):
s7=u+a2(2⋅7−1)
s7=2.5+52(14−1)
s7=2.5+52⋅13
s7=2.5+652
s7=2.5+32.5=35m
Final Answer
The body will travel 35 meters in the seventh second.
---
The distance covered in the nth second of uniformly accelerated motion can be calculated using the formula:
sn=u+a2(2n−1)
where:
- sn is the distance covered in the nth second,
- u is the initial velocity,
- a is the acceleration,
- n is the nth second.
1. For the second second (n=2):
s2=u+a2(2⋅2−1)=u+a2⋅3
Given that s2=10m:
10=u+3a2(Equation 1)
s5=u+a2(2⋅5−1)=u+a2⋅9
Given that s5=25m:
25=u+9a2(Equation 2)
Now we have two equations:
1. 10=u+3a2
2. 25=u+9a2
25−10=(u+9a2)−(u+3a2)
15=9a2−3a2
15=6a2
15=3a
a=5m/s2
10=u+3⋅52
10=u+152
10=u+7.5
u=10−7.5=2.5m/s
Now that we have u=2.5m/s and a=5m/s2, we can find the distance covered in the seventh second (n=7):
s7=u+a2(2⋅7−1)
s7=2.5+52(14−1)
s7=2.5+52⋅13
s7=2.5+652
s7=2.5+32.5=35m
The body will travel 35 meters in the seventh second.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.2
12 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.3
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
Knowledge Check
A body covers a distance of 4 m in 3rd second and 12m in 5th second. If the motion is uniformly accelerated. How far will it travel in the next 3 seconds?
A10 mB30 mC40 mD60 mNewton's second law of motion is
AF=dpdtBF=mvCF=mv2DF=m2v
A body covers 4.9m,14.7m,24.5mand34.3m in the successive seconds of motion. The acceleration of the body is
View SolutionHow does Newton's second law of motion differ from first law of motion ?
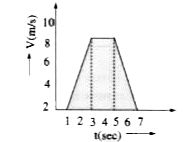
View SolutionFor the velocity - time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the total distance covered by it in all the seven seconds
View SolutionA particle starts moving from rest such that it has uniform acceleration a0 during the 1st second of motion, uniform acceleration a02 during the 2nd second of motion, uniform acceleration a04 during the 3rd second of motion, and so on, such that it has uniform acceleration a02n−1 during the nth second of motion If the displacement of the particle during the 5th second of motion isD5=Ka032 , the value of K is
View SolutionFor rotational motion, the Newton's second law of motion is indicated by :-
View SolutionA trolley moves down a slope from rest with constant acceleration. In the first second of its motion it travels 1.6 m. Its acceleration (in m/s2) is
View Solution
