A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
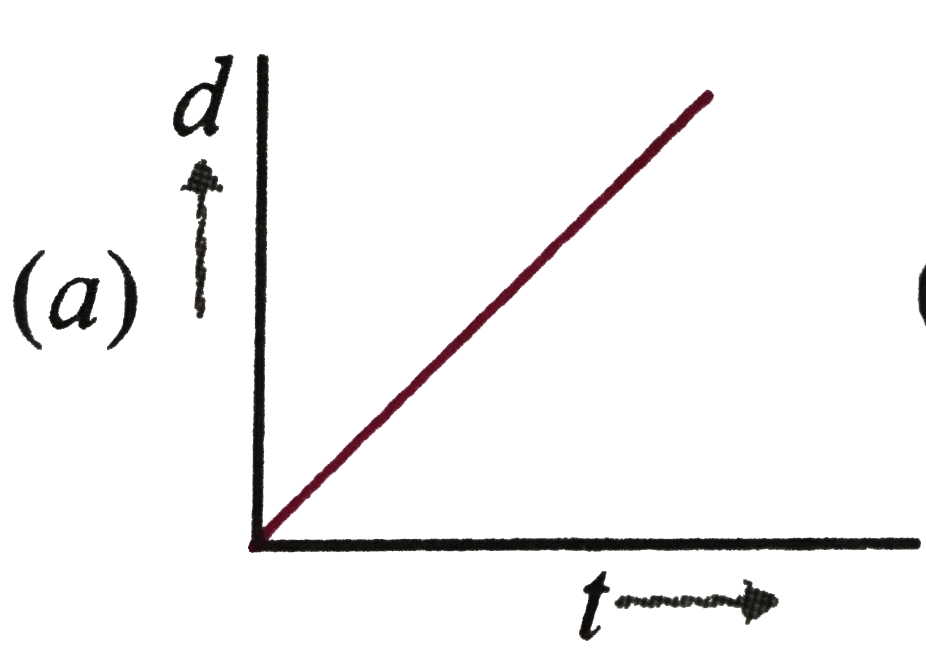
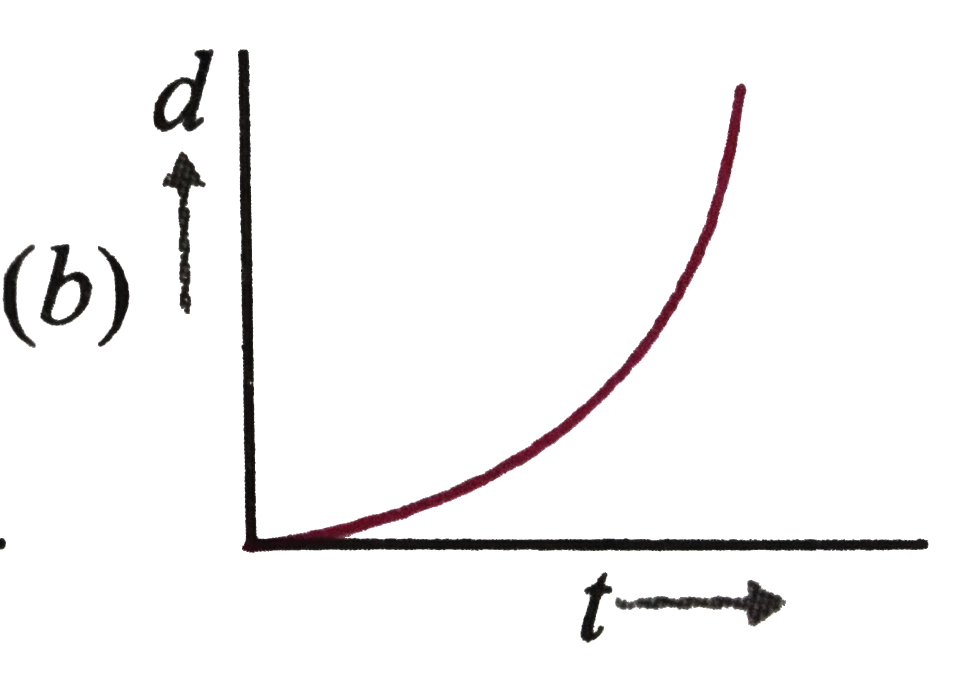

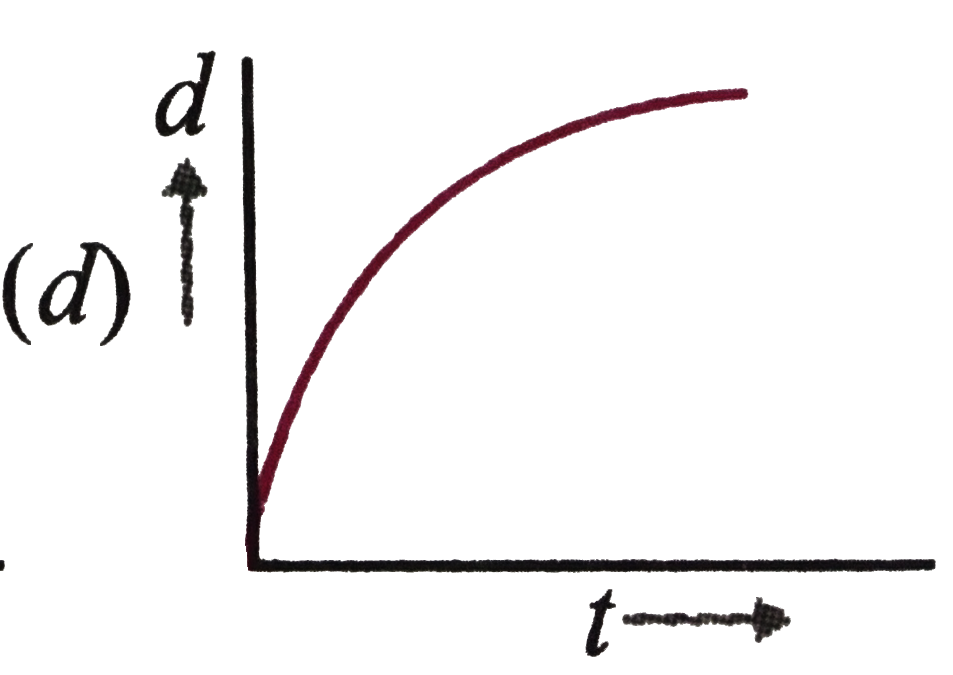
The correct Answer is:B
To solve the problem of finding the correct displacement-time curve for a body moving under the influence of a constant power source, we can follow these steps:
Step 1: Understand the relationship between power, force, and velocity
Power (P) is defined as the product of force (F) and velocity (V):
P=F⋅V
Since the power is constant, we can express this as:
F=PV
Step 2: Relate force to mass and acceleration
According to Newton's second law, force is also given by:
F=m⋅a
where m is the mass of the body and a is its acceleration. Therefore, we can write:
m⋅a=PV
Step 3: Express acceleration in terms of velocity and displacement
Since acceleration a can be expressed as:
a=dVdt
and using the chain rule:
a=VdVdx
we can substitute this into our equation:
m⋅VdVdx=PV
Step 4: Rearranging the equation
Rearranging gives us:
mV2dVdx=P
Now, we can separate variables:
V2dV=Pmdx
Step 5: Integrate both sides
Integrating both sides:
∫V2dV=∫Pmdx
This results in:
V33=Pmx+C
Assuming the initial conditions where V=0 when x=0, we find that C=0. Thus:
V3=3Pmx
Step 6: Express velocity in terms of displacement
Taking the cube root gives us:
V=(3Pm)1/3x1/3
Step 7: Relate velocity to time
Since velocity V is also defined as:
V=dxdt
we can set up the equation:
dxdt=(3Pm)1/3x1/3
Step 8: Separate variables and integrate again
Separating variables gives:
dxx1/3=(3Pm)1/3dt
Integrating both sides:
∫x−1/3dx=(3Pm)1/3∫dt
This results in:
32x2/3=(3Pm)1/3t+C
Again, using initial conditions, we find C=0:
x2/3=23(3Pm)1/3t
Step 9: Solve for displacement
Finally, solving for x:
x=(2Pm)1/2t3/2
Step 10: Identify the displacement-time relationship
The relationship x∝t3/2 indicates that the displacement increases with the power of t3/2. This means the displacement-time graph will be a curve that rises more steeply as time increases.
Conclusion
The correct displacement-time curve will be a curve that represents x as a function of t3/2, which corresponds to option B in the provided diagrams.
---
Power (P) is defined as the product of force (F) and velocity (V):
P=F⋅V
Since the power is constant, we can express this as:
F=PV
According to Newton's second law, force is also given by:
F=m⋅a
where m is the mass of the body and a is its acceleration. Therefore, we can write:
m⋅a=PV
Since acceleration a can be expressed as:
a=dVdt
and using the chain rule:
a=VdVdx
we can substitute this into our equation:
m⋅VdVdx=PV
Rearranging gives us:
mV2dVdx=P
Now, we can separate variables:
V2dV=Pmdx
Integrating both sides:
∫V2dV=∫Pmdx
This results in:
V33=Pmx+C
Assuming the initial conditions where V=0 when x=0, we find that C=0. Thus:
V3=3Pmx
Taking the cube root gives us:
V=(3Pm)1/3x1/3
Since velocity V is also defined as:
V=dxdt
we can set up the equation:
dxdt=(3Pm)1/3x1/3
Separating variables gives:
dxx1/3=(3Pm)1/3dt
Integrating both sides:
∫x−1/3dx=(3Pm)1/3∫dt
This results in:
32x2/3=(3Pm)1/3t+C
Again, using initial conditions, we find C=0:
x2/3=23(3Pm)1/3t
Finally, solving for x:
x=(2Pm)1/2t3/2
The relationship x∝t3/2 indicates that the displacement increases with the power of t3/2. This means the displacement-time graph will be a curve that rises more steeply as time increases.
The correct displacement-time curve will be a curve that represents x as a function of t3/2, which corresponds to option B in the provided diagrams.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - JEE (Main and Advanced)
82 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Comprehension
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Problems For Practice
76 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A body is moving undirectionally under the influence of a source of constatn power. It displacement in time t is proportional to (i) t1/2 (ii) t (iii) t3/2 (iv) t2
View SolutionA body undergoing a straight line motion is under the influence of source of constant power. How does its displacement very with time?
View Solution
Knowledge Check
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
A B
B C
C D
D
A body is moving unidirectionally under the influence of a sources of constant power. The square of its displacement in time t is proportional to
At3Bt2CtD√tAn automobile moves under the action of a constant power supplied by its engine ,it follows that
AThe driving roce and velocity ,both are constantBThe driving force is constant but not the velocityCThe velocity is constant but not the driving forceDBoth driving force as well as velocity vary
What is the nature of the displacement time curve of a body moving with constant acceleration ?
View SolutionWhat is the nature of the displacement-time curve of a body moving with constant velocity ?
View SolutionA body is under the influence of a force such that it delivers a constant power p. The variation of position with time of body as
View SolutionA body moves from point A to B under the action of a force, varying in magnitude as shown in figure. Obtain the work done. Force is expressed in newton and displacement in meter.

View SolutionThe kinetic energy of a body moving along a straight line varies with time as shown in figure. The force acting on the body:

View Solution
