A body Is placed on a turntable. The friction coefficient between the body and the table is μ.
(a) If turntable rotates at constant angular speed ω, find the maximum value of ω for which the block will not slip.
(b) if the angular speed is increased uniformly from rest with an angular acceleration α, at what speed will the block slip?

(a) f=mω2r
fmax=μN=μmg
For no slipping, we have
mω2r≤μmg
ω≤√μgr
ωmax=√μgr (b) This is the case of non-uniform circular motion (As shown in the previous problem), hereat=rα.
√(mω2r)2+(mrα)2≤μmg
ω≤[(μg)2−(rα)2r2]1/4
ωmax=[(μgr)2−α2]1/4

Topper's Solved these Questions
Similar Questions
A block of mass m is kept on a horizontal ruler . The friction coefficient between the ruler and the block is m . The ruler is fixed at one end the block is at a distance L from the fixed end . The ruler is rotated about the fixed end in the horizontal plane through the fixed end
a. What can the maximum angular speed be for which the block does not slip?
b. If the angular speed of the ruler is uniform increase from zero at an angular acceleration a at angular speed will the block slip?
View SolutionA block of mass m is kept on a horizontal ruler . The friction coefficient between the ruler and the block is μ . The ruler is fixed at one end the block is at a distance L from the fixed end . The ruler is rotated about the fixed end in the horizontal plane through the fixed end
a. What can the maximum angular speed be for which the block does not slip?
b. If the angular speed of the ruler is uniform increase from zero at an angular acceleration a at angular speed will the block slip?
View Solution
Knowledge Check
Block B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
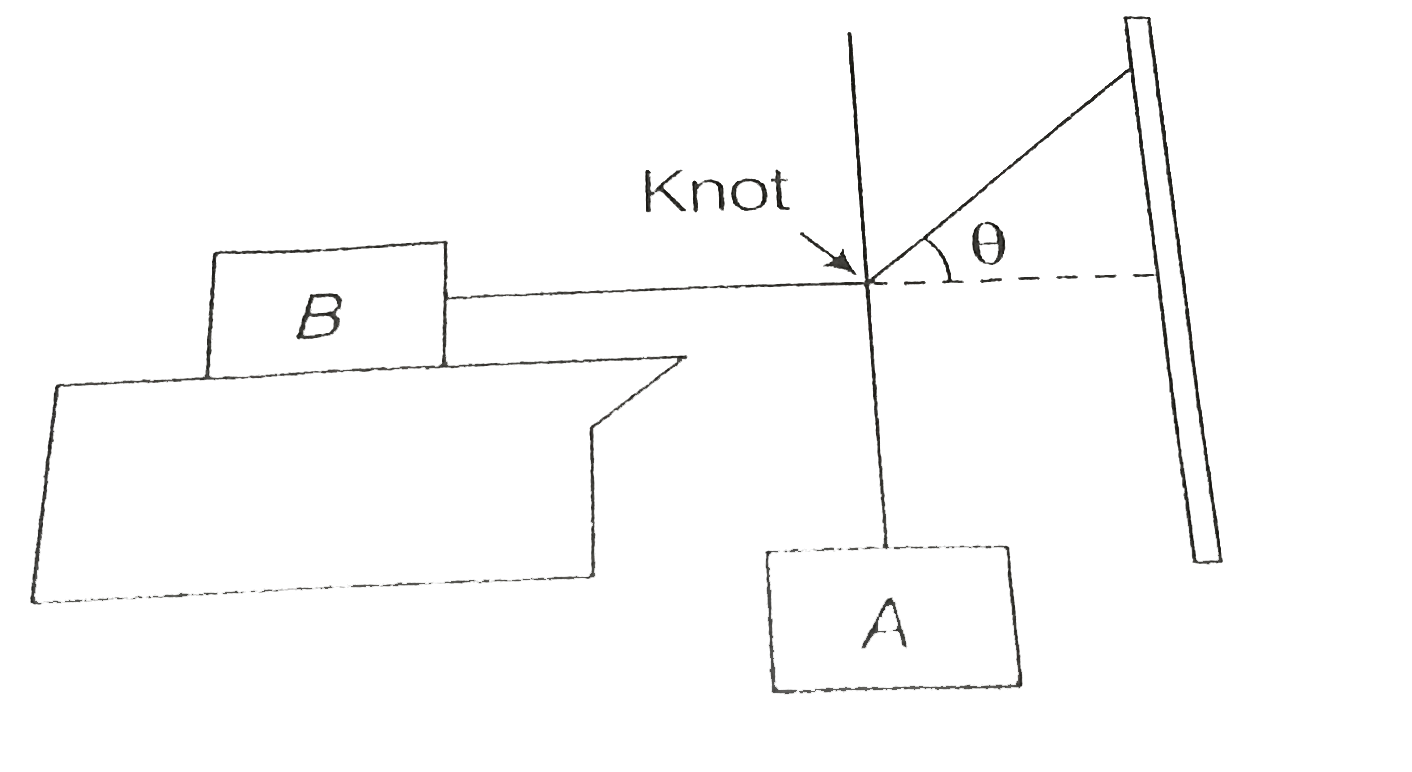 AwtanθμBμwtanθCμw√1+tan2θDμwsinθ
AwtanθμBμwtanθCμw√1+tan2θDμwsinθThe relation between linear speed v, angular speed ω and angular acceleration α in circular motion is
Aα=aωvBα=avωCα=vωaDα=ωavBlock B lying on a table weighs W. The coefficient of static friction between the block and the table is μ. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
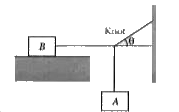 AWtanθμBμWtanθCμW√1+tan2θDμWsinθ
AWtanθμBμWtanθCμW√1+tan2θDμWsinθ
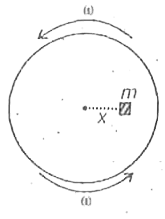
A block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View SolutionA body starting from rest gains an angular speed of 540 r.p.m in 6 second. The angular acceleration of the body is
View SolutionA block of mass m is kept on rough horizontal turn table at a distance r from the center of table. The coefficient of friction between torn table and block is μ Now the turn - table starts rotating with uniform angular acceleration a
a. Find the time after which slipping accure between block and turn - table
b. Find the angle made by friction force at the point of slipping
View SolutionThe coefficient of static friction between a small coin and the surface of a turntable is 0.30 . The turntable rotates at 2rads−1. What is maximum distance from the centre of the turntable at which the coin will not slide ?
View SolutionA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View Solution
