A body is thrown up in a lift with a velocity u relative to the lift, and returns to the lift in time t. Show that the lift's upward acceleration is (2u-gt)/t
To solve the problem step by step, we will analyze the motion of the body thrown upwards in the lift and apply the equations of motion.
Step 1: Understanding the Problem
A body is thrown upwards with an initial velocity u relative to the lift. It returns to the lift after a time t. We need to find the upward acceleration of the lift, denoted as aL.
Step 2: Setting Up the Equation
In the frame of the lift, we can use the equation of motion:
s=ut+12at2
where:
- s is the displacement,
- u is the initial velocity,
- a is the acceleration (which will be the net acceleration of the body relative to the lift).
Since the body returns to the lift, the total displacement s is zero:
0=ut+12at2
Step 3: Determining the Acceleration
The net acceleration a of the body relative to the lift can be expressed as:
a=g−aL
where:
- g is the acceleration due to gravity (acting downwards),
- aL is the upward acceleration of the lift.
Substituting this into the equation gives:
0=ut+12(g−aL)t2
Step 4: Rearranging the Equation
Rearranging the equation, we have:
ut+12(g−aL)t2=0
This can be rewritten as:
ut=−12(g−aL)t2
Step 5: Simplifying the Equation
Multiplying through by -2 to eliminate the fraction:
−2ut=(g−aL)t2
Dividing both sides by t (assuming t≠0):
−2u=(g−aL)t
Step 6: Solving for Lift's Acceleration
Rearranging gives:
g−aL=−2ut
Thus,
aL=g+2ut
This can be rewritten as:
aL=2u−gtt
Conclusion
We have shown that the upward acceleration of the lift is:
aL=2u−gtt
A body is thrown upwards with an initial velocity u relative to the lift. It returns to the lift after a time t. We need to find the upward acceleration of the lift, denoted as aL.
In the frame of the lift, we can use the equation of motion:
s=ut+12at2
where:
- s is the displacement,
- u is the initial velocity,
- a is the acceleration (which will be the net acceleration of the body relative to the lift).
0=ut+12at2
The net acceleration a of the body relative to the lift can be expressed as:
a=g−aL
where:
- g is the acceleration due to gravity (acting downwards),
- aL is the upward acceleration of the lift.
0=ut+12(g−aL)t2
Rearranging the equation, we have:
ut+12(g−aL)t2=0
This can be rewritten as:
ut=−12(g−aL)t2
Multiplying through by -2 to eliminate the fraction:
−2ut=(g−aL)t2
Dividing both sides by t (assuming t≠0):
−2u=(g−aL)t
Rearranging gives:
g−aL=−2ut
Thus,
aL=g+2ut
This can be rewritten as:
aL=2u−gtt
We have shown that the upward acceleration of the lift is:
aL=2u−gtt
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Subjective
29 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.2
12 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A body is thrown up in a lift with a velocity 5ms−1 relative to the lift and the time of flight is found to be 0.8 s. The acceleration with which the lift is moving up is (g=10ms−2)
View SolutionWhen a body is thrown up in a lift with a velocity u relative to the lift, the time of flight is found to be t. The acceleration with which the lift is moving up is
View Solution
Knowledge Check
A man in a lift throws a ball vertically upwards with a velocity v and catches it (i) after t1 second when the lift is ascending with an upward acceleration of 'a' and (ii) after t2 second when the lift is descending downward with the same acceleration 'a'. THe velocity of the ball v is
Ag t1t2B(1/2) g t1t2C2 g t1t2/t1+t2Dg t1t2/t1+t2
A coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View SolutionThe mass of man when standing on the lift is 60 kg. The weight when the lift is moving upwards with acceration 4.9ms−2 is
View SolutionA coin is dropped in a lift. It takes time t1 to reach the floor when lift is stationary. It takes time t2 when lift is moving up with costant acceleration. Then
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
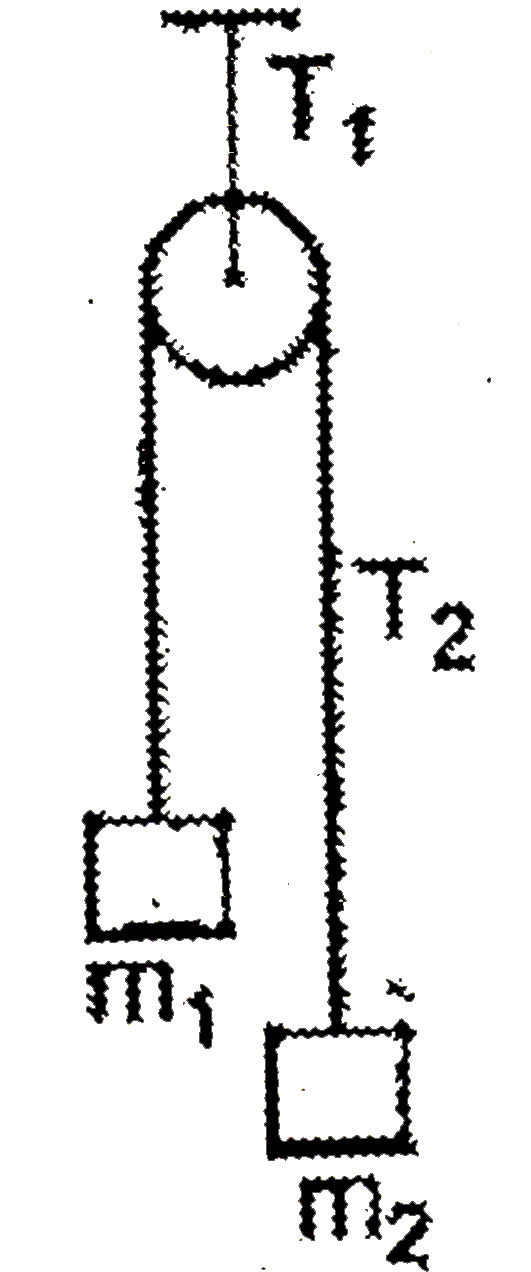
If m1=m2andm1 is moving at a certain instant with velocity v upward with respect to lift and the lift is moving in upward direction with constant acceleration (a<g) then speed of m2 with respect to lift :
View SolutionAn open lift is moving upward with velocity 10m/s. It has an upward acceleration of 2m/s2. A ball is projected upwards with velocity 20m/s relative to ground. Find
(a) time when ball again meets the lift
(b) displacement of lift and ball at that instant.
(c) distance travelled by the ball upto that instant.
Take g=10m/s2
View SolutionA lift is moving up with acceleration a A person inside the ligt throws the ball upwards with a velocity u relativeto hand.
a. What is the time of flight of the ball?
b. What is the maximum height reached by the ball in the lift?

View SolutionA body of mass 50 kg is hung by a spring balance in a lift. Calculate the reading of the balance when :
The lift is ascending with an acceleration of 2m/s2.
View Solution
