Question

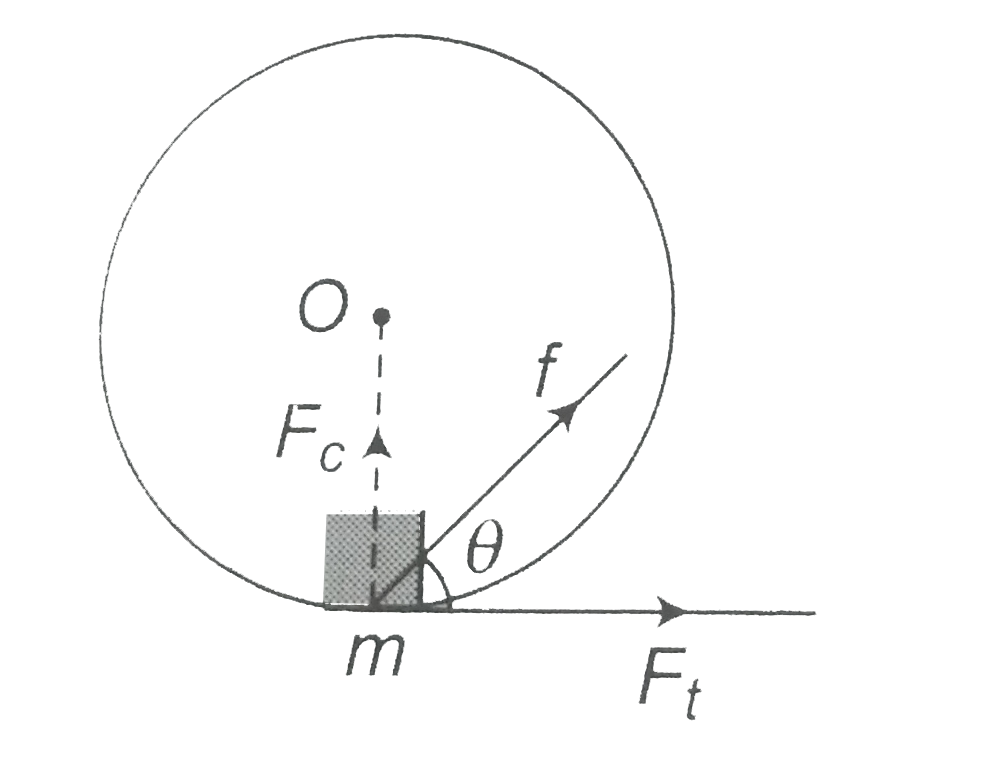
A body moves on a horizontal circular road of radius $r$, with a tangential acceleration $a_t$. The coefficient of friction between the body and the road surface Is $\mu$. It begins to slip when its speed is $v$.
(i) $v^2=\mu rg$
(ii) $\mu g=\left(\frac{v^4}{r^{92}}\right)+a_t)$
(iii) ${\mu }^2{g}^2=(\frac{v^4}{r^2+a_t^2}$
(iv) The force of friction makes an angle ${\tan }^{-1}(v^2/a_{t}r)$ with the direction of motion at the point of slipping.

Options

A. `(i),(ii)`
B. `(ii),(iii)`
C. `(i),(iv)`
D. `(iii),(iv)`

Answer

D

Explanation

`sqrt(F_(c)^(2)+F_(t)^(2))lemumg`
`((mv^(2))/(r ))^(2)+(ma_(t))^(2)le(mu^(2)m^(2)g^(2))`
`(v^(4))/(r^(2))+a_(t)^(2)lemu^(2)g^(2)`
`tan theta=(F_(c))/(F_(t))=(mv^(2)//r)/(ma_(t))=(v^(2))/(a_(t)r)`
`theta=tan^(-1)((v^(2))/(a_(t)r))`