A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

mgk
mgk√1+2hkmg
mgk+mgk√1+2hkmg
None of these
The correct Answer is:b
From the conservation principle,
mgh=12kX20−mgX0
where , X0 is maximum elongation in spring.
⇒12kX20−mgX0−mgh=0
⇒X20−2mgkX0−2mgkh=0
X0=2mgk±√(2mgk)2+4×2mgkh2
Amplitude = elongation in spring for lowest extreme position
- elongation in spring for equilibrium position
=X0−X1=mgk√(1+2hkmg) [∵X1=mgk]
Topper's Solved these Questions
Similar Questions
A body of mass m falls from a height h on to the pan of a spring balance. The masses of the pan and spring are negligible. The spring constant of the spring is k. Having stuck to the pan the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and energy of oscillation.
View SolutionA body of mass m falls from a height h on to the pan of a spring balance, figure, The masses of the pan and spring are negligible. The spring constant of the spring is k. The body gets attached to the pan and starts executing S.H.M. in the vertical direction. Find the amplitude and energy of oscillation.
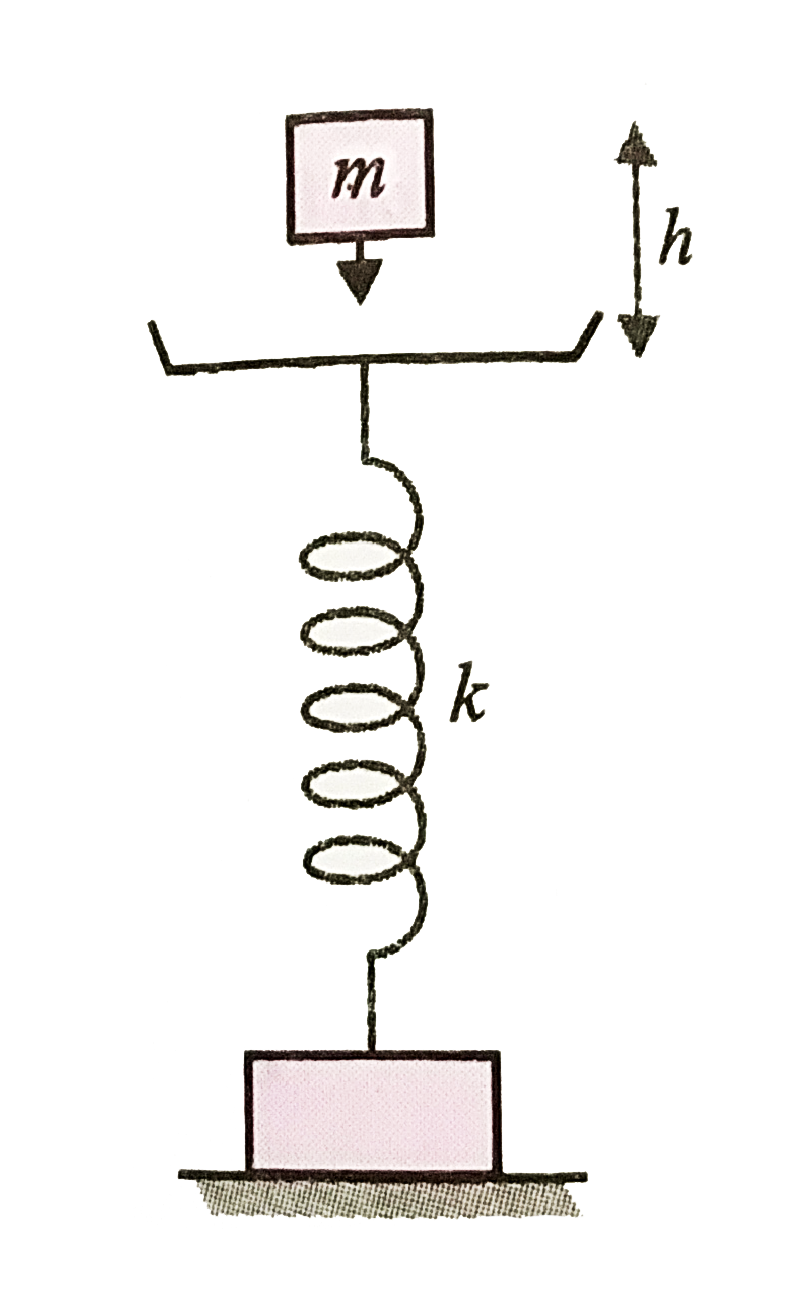
View Solution
Knowledge Check
A body of mass m falls from a height h on a pan ( of negligible mass ) of spring balance as shwon. The spring is ideal and has a spring contant k. Just after striking the pan, the body sticks with the pan and starts oscillatory motion in vertical direction. The velocity of the body at mean position will be
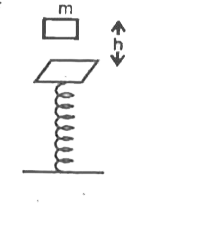 A√2mg2k+2ghB√k2ghmC√mg2k+2ghD√mg2k+4gh
A√2mg2k+2ghB√k2ghmC√mg2k+2ghD√mg2k+4ghA load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is
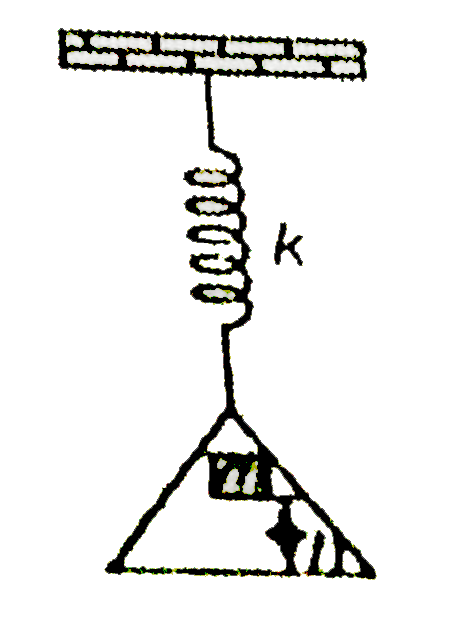 AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
Amgk√1−2hkmgBmgkCmgk+mgk√1+2hkmgDmgk−mgk√1−2hkmg
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
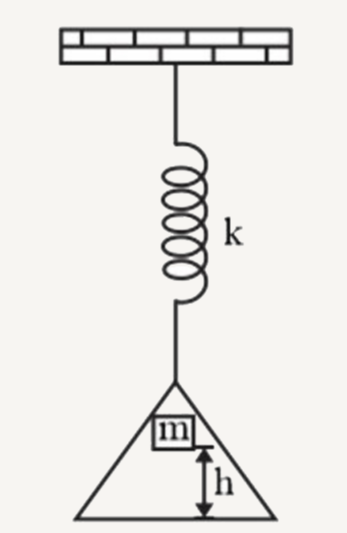
View SolutionA ball of mass m falls from a certain height on the pan of mass M(M>>m) of a spring balance. The rigidity of the s prin is k. Determine the displacement Δx of the point about which the pointer of the balance will oscillate, assuming that the collisions of the ball with the pan are erfectly elastic.
View SolutionA load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is

View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

View SolutionA body is kept in the pan of a spring balance kept in an elevator. The reading of the spring scale will be maximum when the elevator
View Solution
