A body performs a S.H.M. of amplitude a. If the speed of the particle is half of its maximum speed, then the displacement of the particle is
a2
√32a
a
2a
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We are given that a body performs Simple Harmonic Motion (S.H.M.) with an amplitude a. We need to find the displacement x of the particle when its speed v is half of its maximum speed vmax.
Step 2: Write down the formula for maximum speed
The maximum speed vmax in S.H.M. is given by the formula:
vmax=ωa
where ω is the angular frequency and a is the amplitude.
Step 3: Express the speed when it is half of the maximum speed
If the speed of the particle is half of its maximum speed, we can write:
v=12vmax=12ωa
Step 4: Write the formula for speed in S.H.M.
The speed v of a particle in S.H.M. at displacement x is given by:
v=ω√a2−x2
Step 5: Set the two expressions for speed equal
Now we can set the two expressions for speed equal to each other:
ω√a2−x2=12ωa
Step 6: Cancel ω from both sides
Assuming ω≠0, we can divide both sides by ω:
√a2−x2=12a
Step 7: Square both sides to eliminate the square root
Squaring both sides gives:
a2−x2=(12a)2
a2−x2=14a2
Step 8: Rearrange the equation to solve for x2
Rearranging the equation, we get:
x2=a2−14a2
x2=34a2
Step 9: Take the square root to find x
Taking the square root of both sides gives:
x=√34a=√32a
Final Answer
Thus, the displacement of the particle when its speed is half of its maximum speed is:
x=√32a
---
We are given that a body performs Simple Harmonic Motion (S.H.M.) with an amplitude a. We need to find the displacement x of the particle when its speed v is half of its maximum speed vmax.
The maximum speed vmax in S.H.M. is given by the formula:
vmax=ωa
where ω is the angular frequency and a is the amplitude.
If the speed of the particle is half of its maximum speed, we can write:
v=12vmax=12ωa
The speed v of a particle in S.H.M. at displacement x is given by:
v=ω√a2−x2
Now we can set the two expressions for speed equal to each other:
ω√a2−x2=12ωa
Assuming ω≠0, we can divide both sides by ω:
√a2−x2=12a
Squaring both sides gives:
a2−x2=(12a)2
a2−x2=14a2
Rearranging the equation, we get:
x2=a2−14a2
x2=34a2
Taking the square root of both sides gives:
x=√34a=√32a
Thus, the displacement of the particle when its speed is half of its maximum speed is:
x=√32a
Topper's Solved these Questions
Similar Questions
A particle executes SHM with an amplitude 4 cm. Locate the position of point where is speed is half its maximum speed. At what displacement is potential energy equal to kinetic energy?
View SolutionA particle performs linear SHM with amplitude 5 cm and period 2s. Find the speed of the particle at a point where its accleration is half the maximum acceleration.
View Solution
Knowledge Check
A particle starts with S.H.M. from the mean position as shown in the figure. Its amplitude is A and its time period is T. At any instant, its speed is half that of the maximum speed. What is the displacement of the particle at the that point?
 A2A√3B3A√2C√2A3D√3A2
A2A√3B3A√2C√2A3D√3A2A particle perfoms a S.H.M. of amplitude A and period T. It the particle is half way between the mean position and the extreme position, then its speed at that point will be
AπA√3TB3π2ATCπATDπA√32TA particle performs a S.H.M. of amplitude 10 cm and period 12s. What is the speed of the particle 3s, after pas"sin"g through its mean position ?
A5 cm/sB10 cm/sCZeroD7.5 cm/s
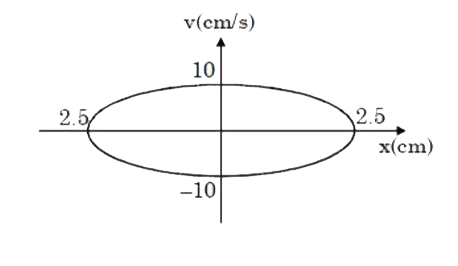
A graph between velocity and displacement of a particle performing SHM is shown. Find the acceleration when the particle is at half of maximum displacement from mean position.
View SolutionA particle starting at the end of its swing performs S.H.M. of amplitude 0.1 m and frequency 60 vibrations per minute. The displacement of the particle at the end of 2 s is
View SolutionThe maximum velocity of a particle performing a S.H.M is v. If the periodic time is made 1/3rd and the amplitude is doubled, then the new maximum velocity of the particle will be
View SolutionA particle starts simple harmonic motion from the mean position. If It's amplitude is A and time period T, then at a certain instant, its speed is half of its maximum speed at this instant, the displacement is
View SolutionA particle starts performing simple harmonic motion. Its amplitude is A. At one time its speed is half that of the maximum speed. At this moment the displacement is
View Solution
