A body starts from rest from a point distant r0 from the centre of the earth. It reaches the surface of the earth whose radius is R. The velocity acquired by the body is
2GM√1R−1r0
√2GM(1R−1r0)
GM√1R−1r0
√GM(1R−1R0)
The correct Answer is:B
GMmr0=12mv2−GMmR
or 12mv2=GMmR−GMmr0
or v2v=GMR−GMr0
or v2=2GM[1R−1r0]
or v=√2GM(1R−1r0)
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Knowledge Check
A body is released from a point of distance R' from the centre of earth. Its velocity at the time of striking the earth will be (R’>Re)
A√2gReB√RegC√2g(R'−Re)D√2gRe(1−ReRr)The escape velocity from the surface of the earth of radius R and density ρ
A2R√2πρG3B2√2πρG3C2π√RgD√2πGρR2A body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
A√2GMRB√2GMR−rC√2GM(r−R)RrDZero
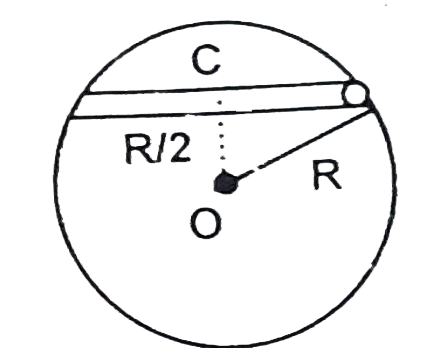
A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View SolutionThe acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
View SolutionThe escape velocity from the surface of the earth is (where RE is the radius of the earth )
View SolutionThe escape velocity of a body from the surface of earth is
View SolutionThe satellite is moving round the earth (radius of earth = R) at a distance r from the centre of the earth. If g is the acceleration due to gravity on the surface of the earth. The acceleration of the satellite will be
View Solution
