A body starts from rest from the origin with an acceleration of 6m/s2 along the x-axis and 8m/s2 along the y-axis. Its distance from the origin after 4 seconds will be
56 m
64m
80 m
128m
The correct Answer is:C
To solve the problem step-by-step, we need to calculate the distance traveled by the body in both the x and y directions after 4 seconds, and then use the Pythagorean theorem to find the total distance from the origin.
Step 1: Identify the given values
- Initial velocity (u) = 0 m/s (since the body starts from rest)
- Acceleration in the x-direction (a_x) = 6 m/s²
- Acceleration in the y-direction (a_y) = 8 m/s²
- Time (t) = 4 seconds
Step 2: Calculate the distance traveled in the x-direction (s_x)
Using the formula for distance under constant acceleration:
sx=ut+12axt2
Since the initial velocity (u) is 0, the equation simplifies to:
sx=12axt2
Substituting the values:
sx=12×6m/s2×(4s)2
sx=12×6×16
sx=48m
Step 3: Calculate the distance traveled in the y-direction (s_y)
Using the same formula:
sy=ut+12ayt2
Again, since the initial velocity (u) is 0:
sy=12ayt2
Substituting the values:
sy=12×8m/s2×(4s)2
sy=12×8×16
sy=64m
Step 4: Calculate the total distance from the origin (r)
Using the Pythagorean theorem:
r=√s2x+s2y
Substituting the values:
r=√(48m)2+(64m)2
r=√2304+4096
r=√6400
r=80m
Final Answer
The distance from the origin after 4 seconds is 80 meters.
---
- Initial velocity (u) = 0 m/s (since the body starts from rest)
- Acceleration in the x-direction (a_x) = 6 m/s²
- Acceleration in the y-direction (a_y) = 8 m/s²
- Time (t) = 4 seconds
Using the formula for distance under constant acceleration:
sx=ut+12axt2
Since the initial velocity (u) is 0, the equation simplifies to:
sx=12axt2
Substituting the values:
sx=12×6m/s2×(4s)2
sx=12×6×16
sx=48m
Using the same formula:
sy=ut+12ayt2
Again, since the initial velocity (u) is 0:
sy=12ayt2
Substituting the values:
sy=12×8m/s2×(4s)2
sy=12×8×16
sy=64m
Using the Pythagorean theorem:
r=√s2x+s2y
Substituting the values:
r=√(48m)2+(64m)2
r=√2304+4096
r=√6400
r=80m
The distance from the origin after 4 seconds is 80 meters.
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Relative Motion
13 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Motion Under Gravity
81 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Uniform Motion
24 Videos
- GRAVITATIONBOOK - ERRORLESS CHAPTER - GRAVITATIONEXERCISE - SET
27 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise
319 Videos
Similar Questions
Knowledge Check
A body starts from rest from the origin with an acceleration of 3m/s(2) along the x-axis and 4m/s2 along the y-axis. Its distance from the origin after 2s will be
A5mB10mC15mD20mA body starts from rest from the origin with an acceleration of 6m/s2 along x axis and 8m/s2 along y axis.The distance from origin after 4 seconds will be
A56mB64mC80mD128mA body starting from rest is moving with a uniform acceleration of 8ms2. Then the distance travelled by it in 5th second will be
A40mB36mC100mDzero
A body starting from test along straight line is traveling with an acceleration of 6ms−1, then the distance traveled by it in the 3rd seconds is ___________m
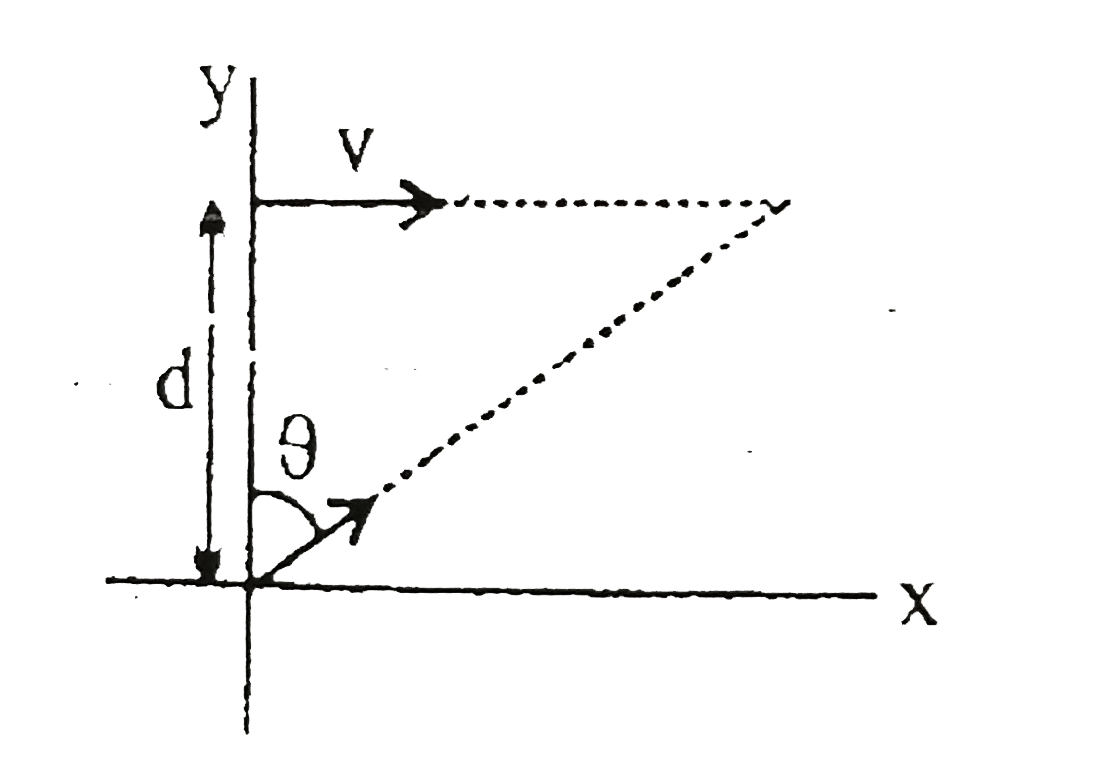
View SolutionA particle moves along a straight line parallel to x-axis at a distancce d=3m from it, with constant speed of v=3m/s. Another particle stats from the origin with constant acceleration a=4m/s2 at an angle θ with y-axis along a straight line at the instant the first particle crosses y-axis. Find 'theta' such that the two particle collide.
View SolutionIf the particle in linear S.H.M. starts from the extreme left position, then its equation of motion is given by
View SolutionA body starting from rest and has uniform acceleration
8m/s2 . The distance travelled by it in5th second will be
View SolutionIf a trolley starts from rest with an accerelaton of 2ms2, the velocity of the body after 4 s would be
View Solution