A body starts sliding down from the top of an inclined plane at an angle θ with the horizontal direction. The first one third of the incline is smooth, the next one third has coefficient of friction μ2 and the last one third has coefficient of friction μ.
If the body comes to rest at the bottom of the plane then the value of μ is
tanθ2
3tanθ2
tanθ
2tantheta
The correct Answer is:D
According to the question, the given situation is shown below,
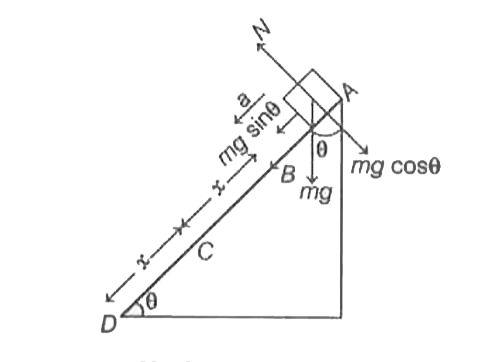
Let mass of body = m and AB = BC = CD = x
[Given in AB, BC and CD plane coefficient of friction respectively 0, μ2 and μ]
For inclined plane AB, friction force, F = 0
So, the net force equation,
mgsinθ−0=ma
or a=gsinθ
Here, from third equation of the motion,
v2=u2+2ax
or v2=2×gsinθ×x=2gxsinθ[∵u=0]
For inclined plane BC, friction force,
F=(μ/2)mgcosθ
So, net force equation,
⇒mgsinθ−(μ/2)mgcosθ=ma.
⇒a.=gsinθ−μ2gcosθ
From third equation of the motion, v2=u2+2a.x
⇒v2=u2+2a.x [∵ in this case u.=v]
⇒v2=2gxsinθ+2(gsinθ−μ2gcosθ)x
v2=4gxsinθ−μgxcosθ
For inclined plane CD, friction force, F=μmgcosθ
So, net force equation,
⇒mgsinθ−μmgcosθ=ma.
⇒a.=gsinθ−μgcosθ
From third equation of the motion,
⇒v..=μ.+2a.x=μ.+2a.x (∵μ.=v.)
⇒0=4gxsinθ−μgxcosθ+2(gsinθ−μgcosθ)x
⇒0=6gxsinθ=3μgxcosθ⇒
6gxsintheta=3ugxcostheta<br>rArr mu=(6gxsintheta)/(3gxcostheta) rArr mu=2tantheta
Topper's Solved these Questions
Similar Questions
A block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
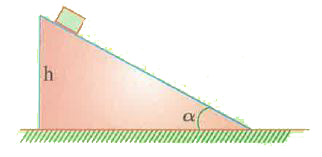
View SolutionA mass m slides down a fixed plane inclined at an angle a to the horizontal plane after covering the entire length of the inclined plane. The height of the inclined plane is h and the coefficient of friction over both surfaces is μ.
View Solution
Knowledge Check
A body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
A1.25ms−2B2.35ms−2C3.4ms−2D4.9ms−2An inclined plane is inclined at an angle θ with the horizontal. A body of mass m rests on it, if the coefficient of friction is μ, then the minimum force that has to be applied to the inclined plane to make the body just move up the inclined plane is
AmgsinθBμmgcosθCμmgcosθ−mgsinθDμmgcosθ+mgsinθA smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
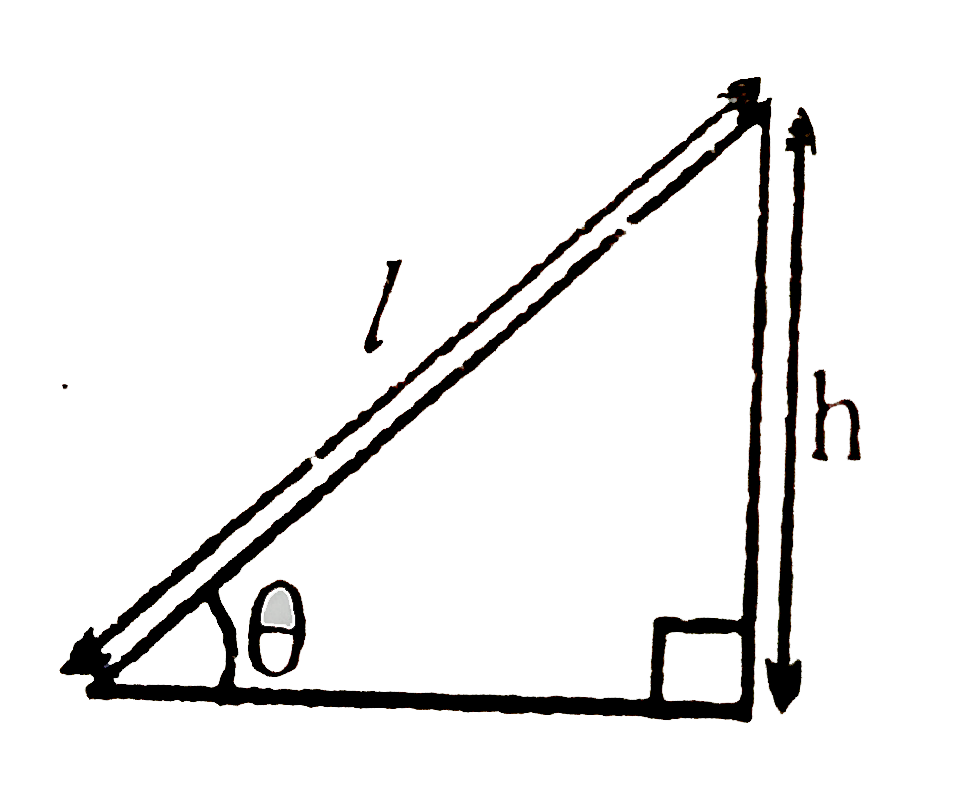 A√2hgB√2lgC√2lgsinθD1sinθ√h2g
A√2hgB√2lgC√2lgsinθD1sinθ√h2g

A small back starts slipping down from a point B on an inclined plane AB, which is making an angle θ with the remaining section CA is rough with a coefficient of friction μ. It is found that bottom (point A) of the inclined plane. If BC=2AC, the coefficient of friction is given by μ=Ktanθ
The value of K is ________.
View Solution
A small back starts slipping down from a point B on an inclined plane AB, which is making an angle θ with the remaining section CA is rough with a coefficient of friction μ. It is found that bottom (point A) of the inclined plane. If BC=2AC, the coefficient of friction is given by μ=Ktanθ
The value of K is ________.
View SolutionThe coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal . As the angle α of the incline is increased the block starts slipping when the angle of inclination becomes θ. The coefficient of static friction between the block and the surface of the inclined plane is or A body starts sliding down at an angle θ to the horizontal. Then the coefficient of friction is equal to
View Solution
