A box weighing 2000 N is to be slowly slid through 20 m on a straigh track having friction coefficient 0.2 with the box. A find the work done by the person pulling the box wilth a chain at angle θ with the horizontal. B. find the work when the person has chosen a value of θ which ensures him the minimum magnitude of the force.
The correct Answer is:A, B, D
To solve the problem, we need to break it down into two parts as specified in the question.
Part A: Work Done by the Person Pulling the Box
1. Identify the Forces Acting on the Box:
- Weight of the box (W) = 2000 N (acting downward).
- Normal force (N) = acts perpendicular to the surface.
- Frictional force (F_friction) = μ * N, where μ = 0.2.
- Pulling force (F) at an angle θ with the horizontal.
2. Calculate the Normal Force:
- The vertical component of the pulling force is F * sin(θ).
- The normal force can be expressed as:
N=W−F⋅sin(θ)
3. Calculate the Frictional Force:
- The frictional force is given by:
Ffriction=μ⋅N=0.2⋅(W−F⋅sin(θ))
4. Determine the Horizontal Component of the Pulling Force:
- The horizontal component of the pulling force is:
Fhorizontal=F⋅cos(θ)
5. Set Up the Equation for Equilibrium:
- Since the box is moving slowly (constant velocity), the net force in the horizontal direction is zero:
Fhorizontal=Ffriction
- Therefore:
F⋅cos(θ)=0.2⋅(2000−F⋅sin(θ))
6. Solve for the Work Done:
- Work done (W) is given by:
W=Fhorizontal⋅d=F⋅cos(θ)⋅20
- Substitute Fhorizontal from the equilibrium equation into the work done equation.
Part B: Work Done at Minimum Force
1. Find the Angle for Minimum Force:
- The minimum force occurs when the frictional force is equal to the horizontal component of the pulling force. This happens when:
tan(θ)=μ
- Therefore:
θ=tan−1(0.2)
2. Substitute θ into the Equations:
- Substitute the value of θ back into the equations for normal force and frictional force to find the minimum force required.
3. Calculate the Work Done:
- Use the value of the minimum force in the work done equation:
Wmin=Fhorizontal⋅20
Final Expressions
- For Part A, the work done can be expressed in terms of F and θ.
- For Part B, the work done will be calculated using the minimum force derived from the angle θ.
- Weight of the box (W) = 2000 N (acting downward).
- Normal force (N) = acts perpendicular to the surface.
- Frictional force (F_friction) = μ * N, where μ = 0.2.
- Pulling force (F) at an angle θ with the horizontal.
- The vertical component of the pulling force is F * sin(θ).
- The normal force can be expressed as:
N=W−F⋅sin(θ)
- The frictional force is given by:
Ffriction=μ⋅N=0.2⋅(W−F⋅sin(θ))
- The horizontal component of the pulling force is:
Fhorizontal=F⋅cos(θ)
- Since the box is moving slowly (constant velocity), the net force in the horizontal direction is zero:
Fhorizontal=Ffriction
- Therefore:
F⋅cos(θ)=0.2⋅(2000−F⋅sin(θ))
- Work done (W) is given by:
W=Fhorizontal⋅d=F⋅cos(θ)⋅20
- Substitute Fhorizontal from the equilibrium equation into the work done equation.
- The minimum force occurs when the frictional force is equal to the horizontal component of the pulling force. This happens when:
tan(θ)=μ
- Therefore:
θ=tan−1(0.2)
- Substitute the value of θ back into the equations for normal force and frictional force to find the minimum force required.
- Use the value of the minimum force in the work done equation:
Wmin=Fhorizontal⋅20
- For Part B, the work done will be calculated using the minimum force derived from the angle θ.
Topper's Solved these Questions
Similar Questions
A block of mass m lying on a horizontal surface (coefficient of static friction =μs) is to be brought into motion by a pulling force F At what angle θ with the horizontal should the force F be applied so that its magnitude is minimum ? Also find the minimum magnitude

View Solutiona block of weight 100 N is slowly slid up on a smooth incline of inclination 370 by as person. Calculate the work done by the person in moving the block through a distance of 2.0 m, if the drivin force is a. parallel to the inclne and b. in the horizontla direction.
View Solution
Knowledge Check
A boy pushes a toy box 2.0 m along the floor by means of a force of 10 N directed downward at an angle of 60∘ to the horizontal.The work done by the boy is
A6JB8JC10JD12J
A box is moved over a horizontal path by applying force F=60N at an angle θ=30∘w.r.t the horizontal. What is the work done during the displacement of the box over a distance of 0.5km.
View SolutionA woman lifts a box weighing 40N from the floor to a shelf 1.5 m above. (a) find the work done by the force (F) the woman exerts on the box (b) Find the work done on the box by its own weight (w) (c ) Find the net work done on the box.
View SolutionA block of mass 5 kg is pulled along a horizontal. The friction coefficient between the block and the surface is 0.5. If the block travels at constant velocity, find the work done by this applied force during a displacement 4 m of the block.
View SolutionA uniform chain of length L and mass M overhangs a horizontal table with its two third part on the table. The friction coefficient between the table and the chain is µ. The work done by the friction during the period the chain slips off the table is [−2kμMgL]. Find the value of k.
View SolutionA 4 kg block is placed on a rough horizontal surface. The coefficient of friction between the block and the surface is μ=0.5. A force F = 18 N is applied on the block making an angle θ with the horizontal. Find the range of values of θ for which the block can start moving.
[Take g=10m/s2,tan−1(2)=63∘sin−1(109√1.25)=84∘]
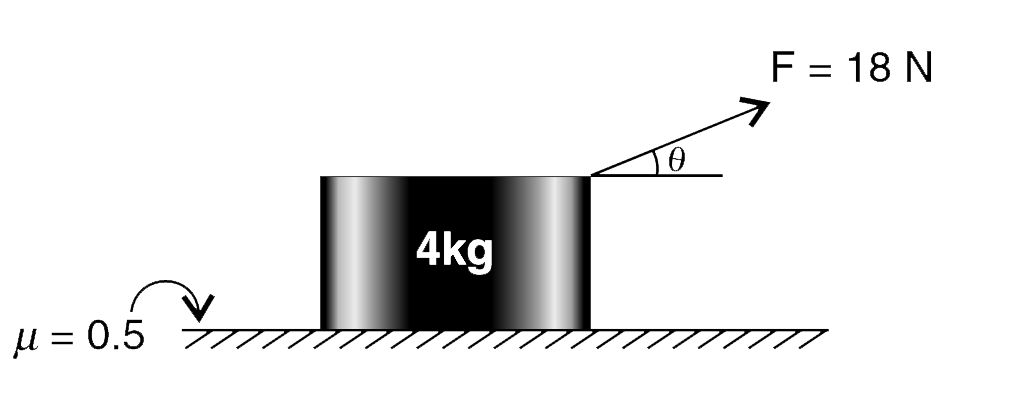
View SolutionA box of bananas weighing 40.0Nrests on a horizontal surface is 0.40 and the coefficient of kinetic friction is 0.20
a. If no horizontal force is applied to the box and the box is at rest , how large is the friction force excered on the box ?
b. What is the magnitude of the friction forces if a monkey applies a horizontal force of 6.0N to the box and the box is initial at rest?
c. What minimum horizontal force must the monkey apply to start the box in motion ?
d. What minimum horizontal force must the monkey apply to keep the box moving at constant velocity once it has been starts?
e. If the monkey applies a horizontal force of 18.0N What is the magnitude of the friction force and what is the box's acceleration ?
View SolutionA box of mass 200 kg is kept on a rough horizontal floor having coefficient of static friction μs=0.25 and coe3fficient kinetic friction μk=0.2. Find the work done by a mam to slide the body slowly through 20 m with a minimum ofrce. Also find the magnitude of the minimum force.
View Solution
