A boy sitting on a merry-round make 200 revolutions per minute . Calculate the angular speed of the merry-go-round.
The correct Answer is:20π3rad/s
To solve the problem of calculating the angular speed of a merry-go-round given that a boy makes 200 revolutions per minute, we can follow these steps:
Step 1: Understand the relationship between revolutions and radians
1 revolution is equal to 2π radians. Therefore, if the boy makes 200 revolutions, the total angle in radians can be calculated as:
Total angle in radians=Number of revolutions×2π=200×2π
Step 2: Convert revolutions per minute to radians per minute
Now, we can calculate the total angle in radians:
Total angle in radians=200×2π=400π radians
Step 3: Convert time from minutes to seconds
Since the angular speed is typically expressed in radians per second, we need to convert the time from minutes to seconds. There are 60 seconds in a minute, so:
Time in seconds=1 minute=60 seconds
Step 4: Calculate angular speed
Angular speed (ω) is defined as the total angle traveled divided by the time taken. Therefore:
ω=Total angle in radiansTime in seconds=400π radians60 seconds
Step 5: Simplify the expression
Now we simplify the expression:
ω=400π60=20π3 radians per second
Final Answer
The angular speed of the merry-go-round is:
ω=20π3 radians per second
---
1 revolution is equal to 2π radians. Therefore, if the boy makes 200 revolutions, the total angle in radians can be calculated as:
Total angle in radians=Number of revolutions×2π=200×2π
Now, we can calculate the total angle in radians:
Total angle in radians=200×2π=400π radians
Since the angular speed is typically expressed in radians per second, we need to convert the time from minutes to seconds. There are 60 seconds in a minute, so:
Time in seconds=1 minute=60 seconds
Angular speed (ω) is defined as the total angle traveled divided by the time taken. Therefore:
ω=Total angle in radiansTime in seconds=400π radians60 seconds
Now we simplify the expression:
ω=400π60=20π3 radians per second
The angular speed of the merry-go-round is:
ω=20π3 radians per second
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (6)
1 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS
2 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (4)
13 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
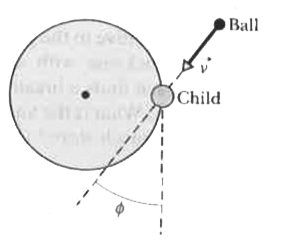
In Fig. 10-86, a 30 kg child stands on the edge of a stationary merry-go-round of radius 2.0 m. The rotational inertia of the merry-go-round about its rotation axis is 150kg⋅m2. The child catches a ball of mass 1.0 kg thrown by a friend. Just before the ball is caught, it has a horizontal velocity →v of magnitude 12 m/s, at angle ϕ=37∘ with a line tangent to the outer edge of the merry-go-round, as shown. What is the angular speed of the merry-go-round just after the ball is caught?
View SolutionIf the wheel of a bus with 50 cm radius makes 280 revolutions per minute, find the speed of the bus in km/h
View Solution
Knowledge Check
A playground merry-go-round of radius R=2.00 has a moment of inertia I=250kg.m2 and is rotating 10.0rev/min about a frictionless, vertical axle. Facing axle, a 25.0−kg child hops onto the merry-go-round and manages to sit down on the edge. The new angular speed of the merry-go-round is.
A5.25rev/minB8.45rev/minC7.14rev/minD3.14rev/minA playground merry-go-round is at rest, pivoted about a frictionless axis. A child of mass m runs along a path tangential to the rim with speed v and jumps on to the merry-go-round. If R is the radius of the merry-go-round and I is its moment of inertia, then the angular velocity of the merry-go-round is
AmvRmR2+IBmvRICmR2mvRDImvRThe diameter of a flywheel is 1.2 m and it makes 900 revolutions per minute. Calculate the acceleration at a point on its rim
A540π2m/s2B270m/s2C360π2m/s2D540m/s2
A cockroach rides the rim of a rotating merry-go-round. If the angular speed of this system (merry-go-round + cockroach) is constant, does the cockroach have (a) radial acceleration and (b) tangential acceleration? If ω is decreasing, does the cockroach have ( c) radial acceleration and (d) tangential acceleration?
View SolutionThe wheels of the locomotive of a train are 2.1 m in radius. They make 75 revolutions in one minute. Find the speed of the train in km per hour.
View SolutionA boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.
View SolutionA child is standing on the edge of a merry-go-round that has the shape of a disk, as shown in the figure. The mass of the child is 40 kg. The merry-go-round has a mass of 200kg and a radius of 2.5 m, and it is rotating with an angular velocity of ω=2.0 radians per second. The child then walks slowly towards the centre of the merry-go-round. What will be the final angular velocity of the merry-go-round when the child reaches the centre? (The size of the child can be neglected)

View Solutionthe force experienced by a body in the merry go-round is
View Solution
