A bullet of mass m is fired at angle with the vertical. The bullet returns to the ground in time t. The total change of momentum equals
The correct Answer is:C
To find the total change of momentum of a bullet fired at an angle θ with the vertical and returning to the ground in time t, we can follow these steps:
1. Understanding the Motion:
- The bullet is fired at an angle θ with the vertical. This means it will follow a projectile motion path and will return to the ground after time t.
2. Identify Forces Acting on the Bullet:
- The only force acting on the bullet during its flight is the gravitational force, which is given by F=mg, where m is the mass of the bullet and g is the acceleration due to gravity.
3. Change in Momentum:
- According to Newton's second law, the change in momentum (Δp) can be calculated using the formula:
Δp=F⋅Δt
- Here, Δt is the total time of flight, which is given as t.
4. Substituting the Values:
- Since the only force acting on the bullet is the gravitational force mg, we can substitute this into the equation:
Δp=mg⋅t
5. Final Result:
- Thus, the total change of momentum of the bullet as it returns to the ground is:
Δp=mgt
Final Answer:
The total change of momentum equals mgt.
- The bullet is fired at an angle θ with the vertical. This means it will follow a projectile motion path and will return to the ground after time t.
- The only force acting on the bullet during its flight is the gravitational force, which is given by F=mg, where m is the mass of the bullet and g is the acceleration due to gravity.
- According to Newton's second law, the change in momentum (Δp) can be calculated using the formula:
Δp=F⋅Δt
- Here, Δt is the total time of flight, which is given as t.
- Since the only force acting on the bullet is the gravitational force mg, we can substitute this into the equation:
Δp=mg⋅t
- Thus, the total change of momentum of the bullet as it returns to the ground is:
Δp=mgt
The total change of momentum equals mgt.
Topper's Solved these Questions
- LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEBOOK - MCGROW HILL PUBLICATIONCHAPTER - LAWS OF MOTION, FRICTION AND ARCHIMEDES' PRINCIPLEEXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- HEATING AND MAGNETIC EFFECTS OF CURRENT BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATING AND MAGNETIC EFFECTS OF CURRENT EXERCISE - HIGHER ORDER THINKING QUESTIONS
34 Videos
- MEASUREMENTBOOK - MCGROW HILL PUBLICATIONCHAPTER - MEASUREMENTEXERCISE - ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
13 Videos
Similar Questions
A man wearing a bullet-proof vest stands still on roller skates. The total mass is 80 kg. A bullet of mass 20 grams is fired at 400 m/s. It is stopped by the vest and falls to the ground. What is then the velocity of the man ?
View SolutionWhat is the total momentum of the bullet and the gun on firing?
View Solution
Knowledge Check
A body of mass m is projected at an angle of 45∘ with the horizontal. If air resistance is negligible, then total change in momentum when it strikes the ground is
A2mvB√mvCmvDmv/√2A ball of mass 'm' is thrown at an angle is 'θ' with the horizontal with an initial velcoity 'u'. The change in its momentum during its flight in a time interval of 't' is .
AmgtBmgtcosθCmgt sinθD½mgtA ball of mass 'm' is thrown at an angle is 'θ' with the horizontal with an initial velocity 'u'.The change in its momentum during its flight in a time interval of 't' is
AmgtBm>cosθCm>sinθD1/2m>.
A bullet fired at an angle of 60∘ with the vertical his the levelled ground at a distance of 200 m . Find the distance at which the bullet will hit the ground when fired at angle of 30∘. (with same speed).
View SolutionA bullet fired at an angle of 60∘ with the vertical hits the ground at a distance of 2 km. Calculate the distance at which the bullet will hit the ground when fired at an angle of 45∘,assuming the speed to be the same.
View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The vertical coordinate of the initial positon of the bob w.r.t. the point of firing of the bullet is
View SolutionA bullet of mass m is fired upward in a direction of angle of projection 60∘ with an initial velocity u. The angular momentum of this vullet when it is crossing highest point with respect to point of projection is
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
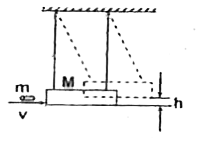
Initial speed of the bullet is
View Solution
