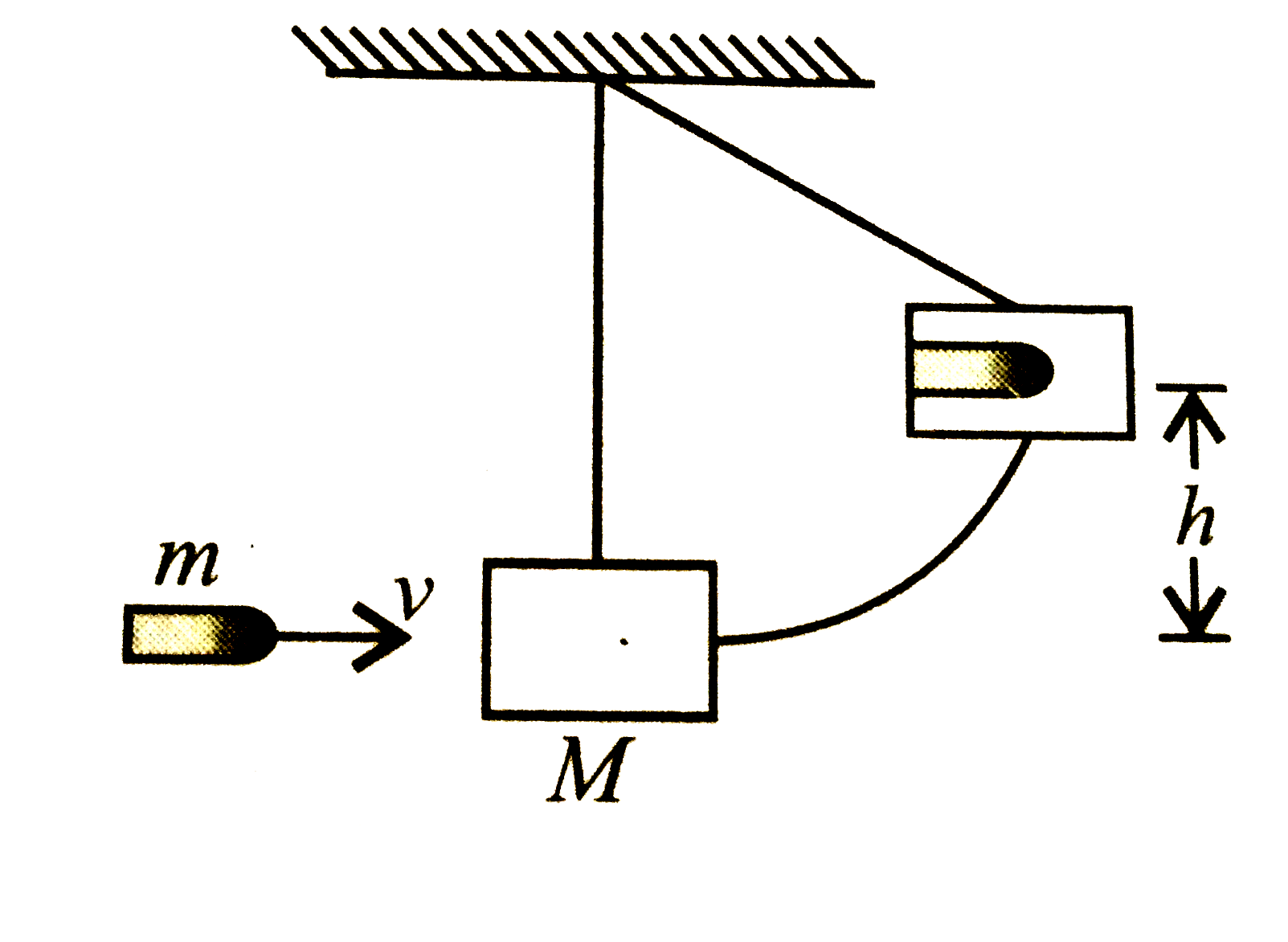
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
v22g(mM+m)2
v22g(M+mm)2
v22g(mM)2
v22g(Mm)2
The correct Answer is:A
The situation is as shown in the figure.
Let V be velocity of the block- bullet system just after collision. Then by the law of conservation of linear momentum, we get
mv=(m+M)V
V=mvm+M
Let the block rises to a height h.
According to law of conservation of mechanical energy, we get
12(m+M)V2=(m+M)gh
h=V22g=v22g(mM+m)2
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - The Potential Energy Of A Spring
6 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - Various Forms Of Energy : The Law Of Conservation Of Energy
6 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - The Concept Of Potential Energy
9 Videos
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A bullet of mass 0.012 kg and horizontal speed 70ms−1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by thin wire. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
View SolutionA bullet of mass m moving horizontally with speed u strikes a suspended wooden block of mass M and gets embedded into it. If block rises to height L2 where L is length of string with which wooden block is connected.The initial velocity(u) of bullet is
View Solution
Knowledge Check
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)mD12Mv2×m(m+M)A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A12mv2×m(m+M)B12mv2×M(m+M)C12mv2×(M+m)MD12mv2(M+m)m
A bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View SolutionA bullet of mass m moving vertically upwards instantaneously with a velocity 'u' hits the hanging block of mass 'm' and gets embedded in it, as shown in the figure. The height through which the block rises after the collision. (assume sufficient space above block) is:
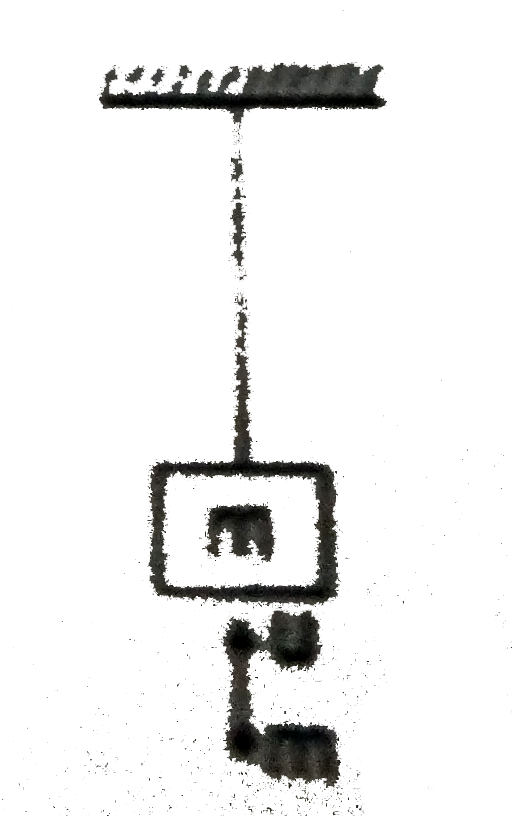
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View SolutionA 50 g bullet moving with velocity 10 m / s strikes a block of mass 950 g at rest and gets embedded in it. The loss in kinetic energy will be
View SolutionA bullet of mass 50 grams going at a speed of 200ms−1 strikes a wood block of mass 950gm and gets embedded in it. The velocity of the block after the impact is
View Solution
