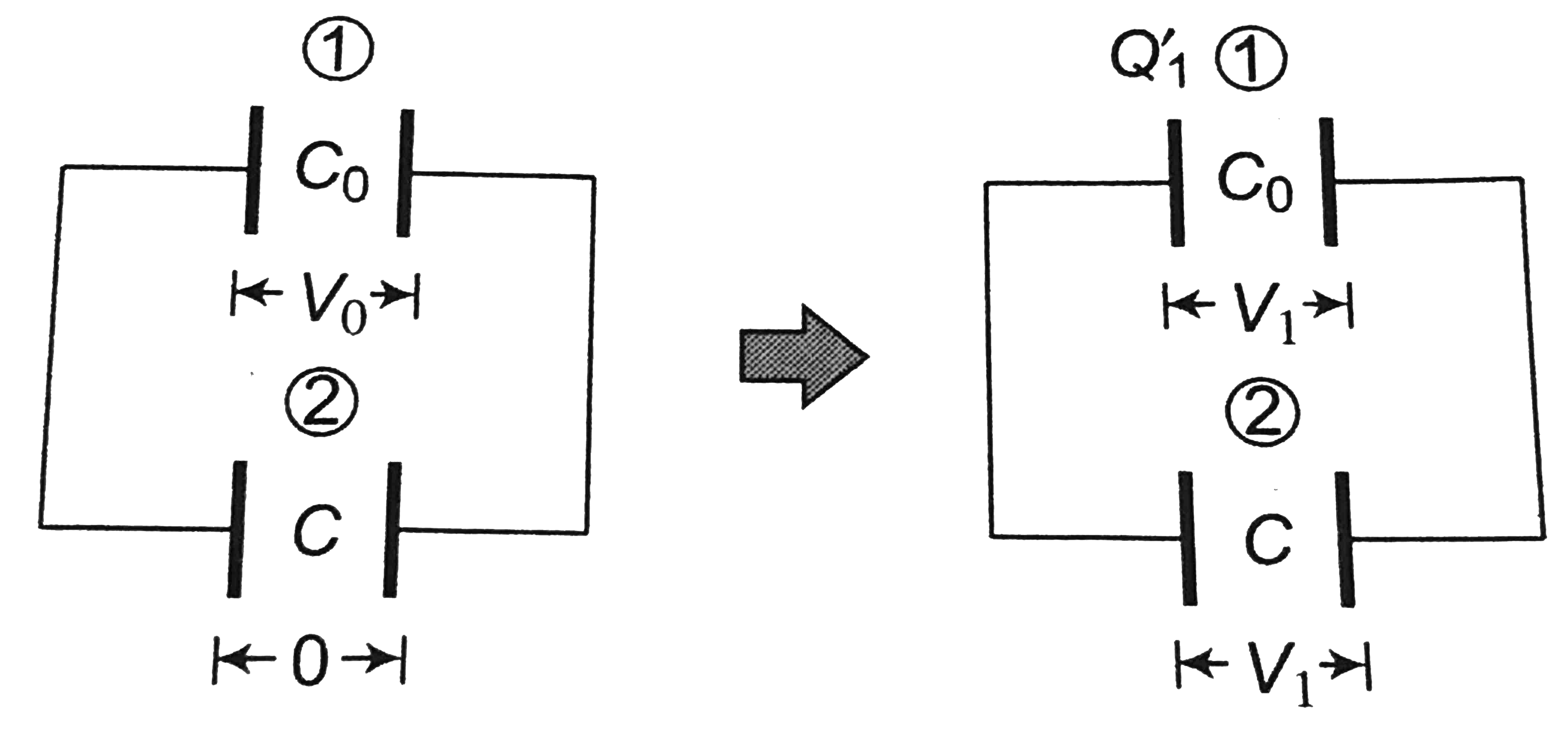
A capacitence of $C_{0}$ is charged to a potential $V_{0}$ and then isolated. $A$ small cpacitor $C$ is then charged from $C_{0}$ , discharged and charged again, the process bing repeated $n$ times. Due to this, potential of the large capacitor is decreased to $V$ . find the capacitance of the small capacitor. is it possible to remove charge on $C_{0}$ completely in this way?

Video Solution

Text Solution

Verified by Experts

First time:
common potential :
$V_{1} = \frac{C_{0} V_{0} + C \times 0}{C_{0} + C} = (\frac{C_{0}}{C_{0} + C}) V_{0}$
Final charge on (i),
$Q'_{1} = C_{0} V_{1} = \frac{C_{0}^{2} V_{0}}{C_{0} + C}$
second time:
Common potential :
$V_{2} = \frac{Q'_{1} + 0}{C_{0} + C} = {(\frac{c_{0}}{C_{0} + C})}^{2} V_{0}$
$n^{t h} time : V_{n} = {(\frac{C_{0}}{C_{0} + C})}^{n} V_{0}$
$V = {(\frac{C_{0}}{C_{0} + C})}^{n} V_{0}$
$\frac{C_{0}}{C_{0} + C} = {(\frac{V}{V_{0}})}^{\frac{1}{n}} \Rightarrow \frac{C + C_{0}}{C_{0}} = {(\frac{V_{0}}{V})}^{1 / n}$
$C = C_{0} ⎡ ⎣ {(\frac{V_{0}}{V})}^{\frac{1}{n}} - 1 ⎤ ⎦$
The charge on $C_{0}$ cannot be removed completely in this way.

Updated on:21/07/2023

A capacitor of capacitance $C_{0}$ is charged to a voltage $V_{0}$ and then isolated. An uncharged capacitor C is then charged from $C_{0}$ , discharged and charged again , the process is repeated n times. Due to this, potential of the $C_{0}$ is decreased to V, then value of C is :
A $C_{0} {[V_{0} / V]}_{0}^{1 / n}$
B $C_{0} [{(V_{0} / V)}_{0}^{1 / n} - 1]$
C $C_{0} [(V_{0} / V) - 1]$
D $C_{0} [V / V_{0}^{n} + 1]$
A capacitor of capacitance $C_{0}$ is charged to potential $V_{0}$ . Now it is connected to another uncharged capacitor of capacitance $\frac{C_{0}}{2}$ . Calculate the heat loss in this process.
A $\frac{1}{2} C_{0} V_{0}^{2}$
B $\frac{1}{3} C_{0} V_{0}^{2}$
C $\frac{1}{6} C_{0} V_{0}^{2}$
D $\frac{1}{8} C_{0} V_{0}^{2}$
The potentials of the two plates of capacitor are $+ 10 V$ and $- 10 V$ . The charge on one of the plate is $40 C$ . The capacitance of the capacitor is
A $2 F$
B $4 F$
C $0.5 F$
D $0.25 F$