A capacitor has a capacitance of 8.5μF. How much charge must be removed so as to reduce the potential difference between its plates by 50V?
The correct Answer is:4.25×10−4C
To solve the problem of how much charge must be removed from a capacitor with a capacitance of 8.5μF to reduce the potential difference between its plates by 50V, we can follow these steps:
Step 1: Understand the relationship between charge, capacitance, and voltage
The relationship between charge (Q), capacitance (C), and voltage (V) is given by the formula:
Q=C⋅V
Where:
- Q is the charge in coulombs,
- C is the capacitance in farads,
- V is the voltage in volts.
Step 2: Define the initial conditions
Let the initial voltage across the capacitor be V0. The initial charge on the capacitor can be expressed as:
Q0=C⋅V0
Step 3: Define the final conditions after removing charge
After removing charge Q, the new voltage across the capacitor becomes:
V=V0−50
The new charge on the capacitor can then be expressed as:
Q=Q0−Q
Step 4: Set up the equation for the new charge
Using the capacitance formula for the new voltage, we have:
Q=C⋅V=C⋅(V0−50)
Substituting Q0 into the equation gives:
Q0−Q=C⋅(V0−50)
Step 5: Substitute Q0 and simplify
Substituting Q0=C⋅V0 into the equation:
C⋅V0−Q=C⋅(V0−50)
This simplifies to:
Q=C⋅50
Step 6: Calculate the charge to be removed
Now we can substitute the value of C:
Q=8.5μF⋅50V
Convert 8.5μF to farads:
Q=8.5×10−6F⋅50V
Calculating this gives:
Q=425×10−6C=425μC
Final Answer
The amount of charge that must be removed to reduce the potential difference by 50V is:
425μC
---
The relationship between charge (Q), capacitance (C), and voltage (V) is given by the formula:
Q=C⋅V
Where:
- Q is the charge in coulombs,
- C is the capacitance in farads,
- V is the voltage in volts.
Let the initial voltage across the capacitor be V0. The initial charge on the capacitor can be expressed as:
Q0=C⋅V0
After removing charge Q, the new voltage across the capacitor becomes:
V=V0−50
The new charge on the capacitor can then be expressed as:
Q=Q0−Q
Using the capacitance formula for the new voltage, we have:
Q=C⋅V=C⋅(V0−50)
Substituting Q0 into the equation gives:
Q0−Q=C⋅(V0−50)
Substituting Q0=C⋅V0 into the equation:
C⋅V0−Q=C⋅(V0−50)
This simplifies to:
Q=C⋅50
Now we can substitute the value of C:
Q=8.5μF⋅50V
Convert 8.5μF to farads:
Q=8.5×10−6F⋅50V
Calculating this gives:
Q=425×10−6C=425μC
The amount of charge that must be removed to reduce the potential difference by 50V is:
425μC
Topper's Solved these Questions
- CAPACITORSBOOK - SL ARORACHAPTER - CAPACITORSEXERCISE - Problem From Competitive Examinations
17 Videos
- ATOMS, NUCLEI AND MOLECULESBOOK - SL ARORACHAPTER - ATOMS, NUCLEI AND MOLECULESEXERCISE - Problems For Self Practice
87 Videos
- CHEMICAL EFFECT OF CURRENTBOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B
5 Videos
Similar Questions
A capacitor has a capacitance of 7.28μF. What amount of charge must be placed on each of its plates to make the potential difference between its plates equAl to 25.0V?
View SolutionA charge of 1μC is given to one plate of a parailel - plate capacitor of capacitance 0.1μF and a charge of 2μC is given to the other plate . Find the potential difference developed between the plate .
View Solution
Knowledge Check
One plate of a capacitor of capacitance 2μF has total charge +10μC and its other plate has total charge +40mUC. The potential difference between the plates is (in Volt).
A7.5B15C25D50A capacitor of capacitance 500μF is charged at the rate of 100μC/s. The time in which the potential difference will become 20V, is :
A100sB50 sC20 sD10 sIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
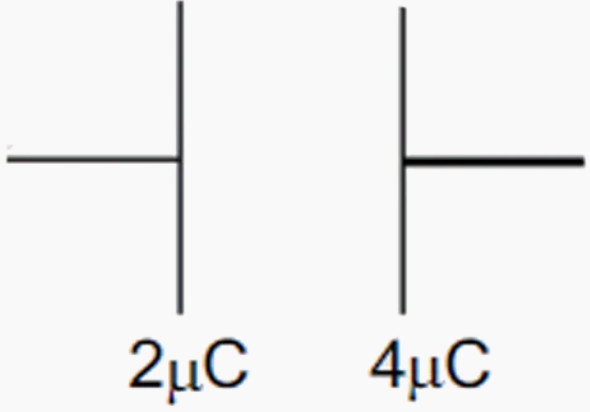 A2 voltB1 voltC4 voltD3 volt
A2 voltB1 voltC4 voltD3 volt
A parallel plate capacitor whose capacitance C is 13.5pF is charged by a battery to a potential difference V=12.5V between its plates. The charging battery is now disconnected, and a porcelain slab (k=6.50) is slipped between the plates.
(a) What is the potential energy of the capacitor before the slab is inserted?
(b) What is the potential energy of the capacitor slab device after the slab is inserted?
View SolutionA parallel plate capacitor of capacitance C has been charged, so that the potential difference between its plates is V. Now, the plates of this capacitor are connected to another uncharged capacitor of capacitance 2C. Find the common potential acquired by the system and loss of energy.
View SolutionA parallel plate capacitor having capacitance 12pF is charged bya battery to a potential difference of 10V between its plates. The charging battery is now disonnected and a porcelain slab of dielectric constant 6.5 is slipped between the plates. The work done by the capacitor on the slab is
View SolutionThe plates of capacitor are charged to a potential difference of 100V and then connected across a resistor.When the potential difference between the plates of the capacitor is 60V ,what is the fraction of the stored energy which has been dissipated?
View SolutionThe ratio of potential differences between 1μFand5μF capacitors is
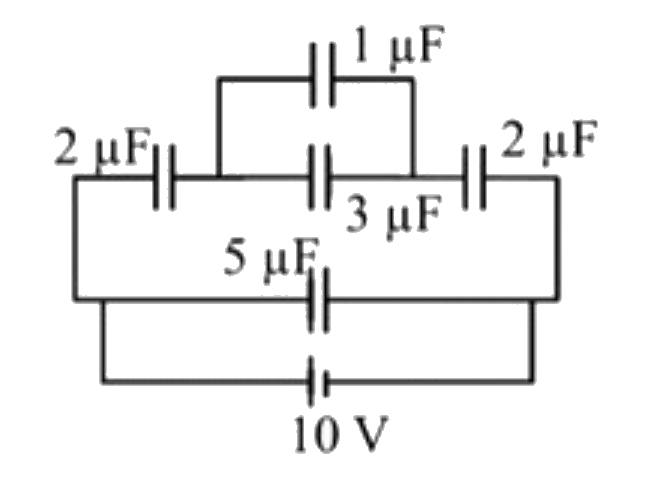
View Solution
