A capacitor is made of two circular plates of radius R each, separated by a dJstance d R. The capacitor is connected to a constant voltage. A th.in conducting disc of radius r R and thickness t R is placed at a centre of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m. Solution in Gujrati
Initially the thin conducting ruse is placed at the centre of the bottom plate. Whole plate is equipotential surface. If electric field applied to disc is E, then the electric field between the plates of capacitor
Let charge q. is transferred to the disc during the process. Hence, by Gaussu.s law,
The repulsive force acting on the disc is in upward direction, so
F= qE
=
This repulsive force will be balanced by weight (mg) of disc,
= mg
If the disc is to be lifted then minimum voltage,
is required equation .
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( Multiple Choice Questions (MCQs) )
93 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( MCQs asked in Cometitive Exams )
39 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section C ( NCERT Exemplar Solution ) (Short ,Aswer Type Questions )
5 Videos
- ELECTROMAGNETIC WAVESBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - BOARD.S QUESTION PAPER MARCH - 2020 (PART - B) SECTION - C
5 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION D Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams) MCQs asked in Board Exam and GUJCET
7 Videos
Similar Questions
When a unit positive charge moves from one point to another point in an electric field, work done on it ......
View SolutionCapacitance of a capacitor 100 μ F. The work is done for depositing chargc 8×10−18 C on it will be .........
View SolutionProve that a closed equipotential surface with no charge within ilself must enclose an equipotential volume.
View SolutionDetermine the current in each branch of the given network.

View SolutionAt a place on earth the vertical component of earth's magnetic field is √3 times its horizontal component. The angle of dip at this place is …...
View SolutionAn elector is moving in a circular orbit of radius R with an angular acceleration alpha . At the centre of the orbit is kept a conducting loop of radius r, (r lt lt R) . The e.m.f induced in the smaller loop due to the motion of the electron is
View SolutionA capcitor is made of two circular paltes of radius R each, separated by a distance d<<R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t<<r is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc si m.
View SolutionA round dielectric disc of radius R and thickness d is statically polarized so that it gains the uniform polarzation P . With the vector P lying in the plane of the disc. Find the strength E of the electric field at the centre of the disc if d lt lt R .
View SolutionA steel ring is to be fitted on a wooden disc of radius R and thickness d. The inner radius of the ring is r which is slightly smaller than R. The outer radius of the ring is r + b and its thickness is d (same as the disc). There is no change in value of b and d after the ring is fitted over the disc, only the inner radius becomes R. If the Young’s modulus of steel is Y, calculate the longitudinal stress developed in it. Also calculate the tension force developed in the ring.
[Take b<<r]
View SolutionFind V and E at : (Q is a point charge kept at the centre of the non-conducting neutral thick sphere of inner radius 'a' and outer radius 'b') (dielectric constant =in_(r) ) (i) 0 lt r lt a " " (ii) a le r lt b " " (iii) r ge b
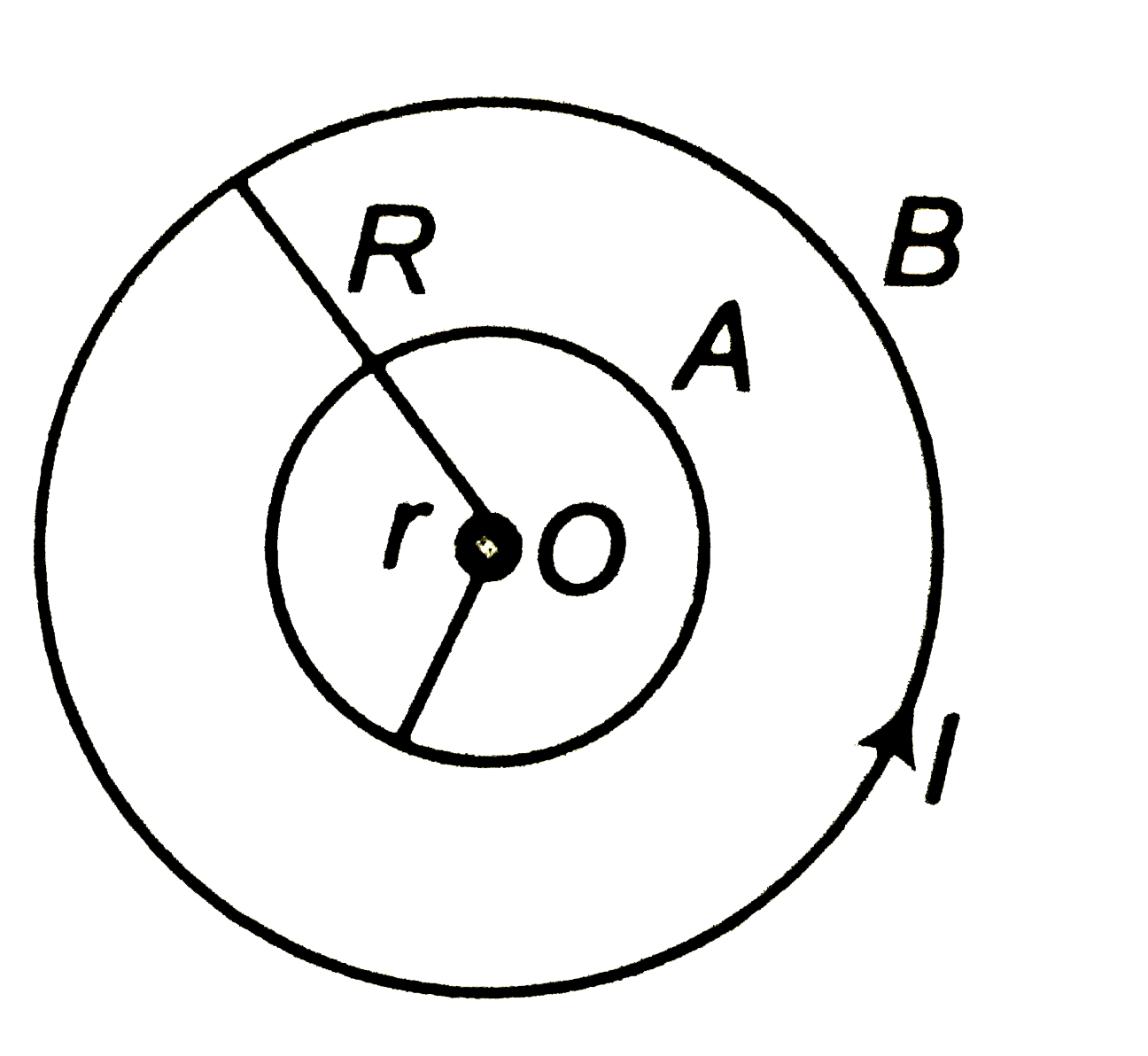
View SolutionO is the centre of two coplanar concentric circular conductors, A and B, of radii r and R respectively as shown in the figure. Here, r<<<R. The mutual inductance of the system of the conductors can be given by
View SolutionTwo concentric co - planar circular loops of radius R and r (lt lt R) are placed as shown in the figure. The mutual inductance of the system will be
View Solutionr < < R எனில், I = __________________
View Solutionएक संधारित्र d<<R दूरी द्वारा अलग की गई एक ही त्रिज्या R की दो वृत्तीय प्लेटों का बना है। संधारित्र को किसी नियत वोल्टेज से जोड़ा गया है। r<<R त्रिज्या तथा मोटाई t<<r की एक पतली चालक चकती को सबसे निचली प्लेट (Bottom plate) के केन्द्र पर रखा गया है। यदि चकती का द्रव्यमान m हो, तो चकती को उठाने के लिए आवश्यक न्यूनतम वोल्टता होगी -
View SolutionTwo small satellites move in circular orbits around the earth, at distances r and r + Ar from the centre of the earth. Their time periods of rotation are T and T + DeltaT. (Deltar lt lt r.DeltaT lt lt T)
View Solution
