A capacitor of capacitance C, which is initially uncharged , is connected with a battery of emf . Find the heat dissipated in the circuit during the process of charging .
To find the heat dissipated in the circuit during the charging of a capacitor, we can follow these steps:
Step 1: Understand the Initial and Final Conditions
Initially, the capacitor is uncharged, which means:
- Charge (Q_initial) = 0
- Voltage across the capacitor (V_initial) = 0
When the capacitor is fully charged, the final conditions are:
- Charge (Q_final) = C * ε (where ε is the emf of the battery)
- Voltage across the capacitor (V_final) = ε
Step 2: Calculate the Potential Energy Stored in the Capacitor
The potential energy (U) stored in a capacitor is given by the formula:
U=12CV2
Substituting V with ε (the emf of the battery), we get:
U=12Cε2
Step 3: Calculate the Total Work Done by the Battery
The work done (W) by the battery in charging the capacitor can be calculated as:
W=Q⋅V
Where Q is the final charge on the capacitor and V is the voltage across the battery. Therefore:
W=Qfinal⋅ε=(Cε)⋅ε=Cε2
Step 4: Relate Work Done, Stored Energy, and Heat Dissipated
The work done by the battery is equal to the sum of the energy stored in the capacitor and the heat dissipated (H) in the circuit:
W=U+H
Substituting the values we calculated:
Cε2=12Cε2+H
Step 5: Solve for Heat Dissipated
Rearranging the equation to find H:
H=Cε2−12Cε2
H=12Cε2
Conclusion
The heat dissipated in the circuit during the process of charging the capacitor is:
H=12Cε2
---
Initially, the capacitor is uncharged, which means:
- Charge (Q_initial) = 0
- Voltage across the capacitor (V_initial) = 0
- Charge (Q_final) = C * ε (where ε is the emf of the battery)
- Voltage across the capacitor (V_final) = ε
The potential energy (U) stored in a capacitor is given by the formula:
U=12CV2
Substituting V with ε (the emf of the battery), we get:
U=12Cε2
The work done (W) by the battery in charging the capacitor can be calculated as:
W=Q⋅V
Where Q is the final charge on the capacitor and V is the voltage across the battery. Therefore:
W=Qfinal⋅ε=(Cε)⋅ε=Cε2
The work done by the battery is equal to the sum of the energy stored in the capacitor and the heat dissipated (H) in the circuit:
W=U+H
Substituting the values we calculated:
Cε2=12Cε2+H
Rearranging the equation to find H:
H=Cε2−12Cε2
H=12Cε2
The heat dissipated in the circuit during the process of charging the capacitor is:
H=12Cε2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples10videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.113videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
Similar Questions
A capacitor of capacitance C which is initially charged up to a potential differnce ε is connected with a battery of emf ε2 such that the positive terminal of the battery is connected with the positive plate of the capacitor. Find the heat loss in the circuit the process of charging.
View SolutionA capacitor of capacitance C, which is initially charged up to a potential differnce ε, is connected with a battery of emf ε/2 such that the positive terminal of the battery is connected with the positive plate of the capacitor. After a long time.
i. find the total charge flow through the battery
ii. find the total work done by the battery
iii. Find the heat dissipated in the circuit during the process of charging.View SolutionA capacitor of capacitance C carrying charge Q is connected to a source of emf E. Finally, the charge on capacitor would be
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance C is charged by connecting it to a battery of emf epsilon. The capacitor is now disconnected and reconnected to the battery with the polarity reversed. Calculate the heat developed in the connecting wires.
View SolutionA capacitor of capacitance C has charge Q. it is connected to an identical capacitor through a resistance. The heat produced in the resistance is
View SolutionThe capacitor C1 in the flgure shown initially carries a charge q0. When the switches S1 and S2 are closed,capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
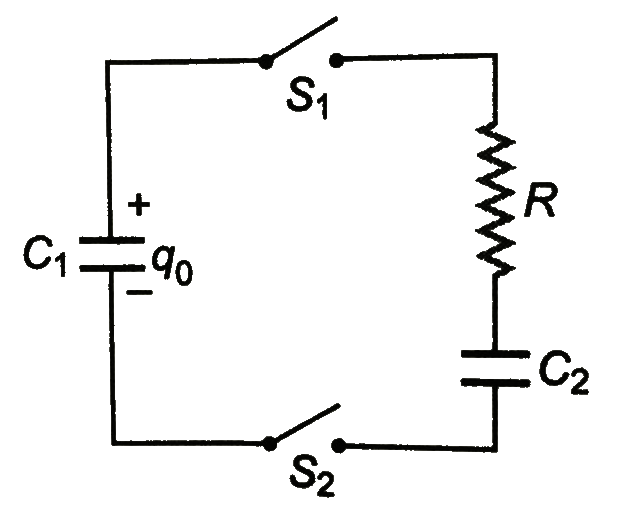
the total heat dissipated in the circuit during the discharging process of C1 isView SolutionA 2μF capacitor that was initially uncharged is connected to a battery of EMF 100V and a resistance and the switch is closed. The heat generated in the resistance until the capacitor becomes fully charged is (in mJ):
View SolutionTwo parallel plate capacitors of capacitance C each are connected in series with a battery of emf ε. Then, one of the capacitors is filled with a dielectric of dielectric constane K.
i. Find the change in electric field in the two capacitors, if any
ii. What amount of charge flows through the battery?
iii Find the change in the energy stored in the circuit, if any.View Solution

