A capacitor with stored energy 4.0J is connected with an identical capacitor with no electric field in between . Find the total energy stored in the two capacitors .
To solve the problem of finding the total energy stored in two identical capacitors, we can follow these steps:
1. Identify the Given Information:
- We have one capacitor with stored energy U1=4.0J.
- The second capacitor is identical but initially has no electric field, meaning it has no stored energy.
2. Understand the Capacitors' Configuration:
- When two identical capacitors are connected, the charge will redistribute between them.
- Let the capacitance of each capacitor be C.
3. Calculate the Charge on the First Capacitor:
- The energy stored in a capacitor is given by the formula:
U=Q22C
- Rearranging this formula to find the charge Q on the first capacitor, we have:
Q2=2CU1
- Substituting U1=4.0J:
Q2=2C⋅4.0=8C
4. Charge Distribution:
- When the two capacitors are connected, the total charge Q will be equally distributed between the two capacitors since they are identical.
- Therefore, the charge on each capacitor after connection will be:
Qeach=Q2=√8C2=√82√C=√2C
5. Calculate the Energy Stored in Each Capacitor After Connection:
- The energy stored in each capacitor after the charge redistribution can be calculated using the energy formula:
Ueach=(Qeach)22C
- Substituting Qeach=√2C:
Ueach=(√2C)22C=2C2C=1.0J
6. Calculate the Total Energy Stored in Both Capacitors:
- The total energy stored in both capacitors is:
Utotal=Ueach+Ueach=1.0J+1.0J=2.0J
Final Answer:
The total energy stored in the two capacitors is 2.0J.
---
- We have one capacitor with stored energy U1=4.0J.
- The second capacitor is identical but initially has no electric field, meaning it has no stored energy.
- When two identical capacitors are connected, the charge will redistribute between them.
- Let the capacitance of each capacitor be C.
- The energy stored in a capacitor is given by the formula:
U=Q22C
- Rearranging this formula to find the charge Q on the first capacitor, we have:
Q2=2CU1
- Substituting U1=4.0J:
Q2=2C⋅4.0=8C
- When the two capacitors are connected, the total charge Q will be equally distributed between the two capacitors since they are identical.
- Therefore, the charge on each capacitor after connection will be:
Qeach=Q2=√8C2=√82√C=√2C
- The energy stored in each capacitor after the charge redistribution can be calculated using the energy formula:
Ueach=(Qeach)22C
- Substituting Qeach=√2C:
Ueach=(√2C)22C=2C2C=1.0J
- The total energy stored in both capacitors is:
Utotal=Ueach+Ueach=1.0J+1.0J=2.0J
The total energy stored in the two capacitors is 2.0J.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
A capacitor with stored energy 4.0J is connected with an identical capacitor with no electric fileld in between . Find the total energy stored in the two capactors .
View SolutionThe energy stored in 4μF capacitors is
View SolutionFind the charge stored in the capacitor.
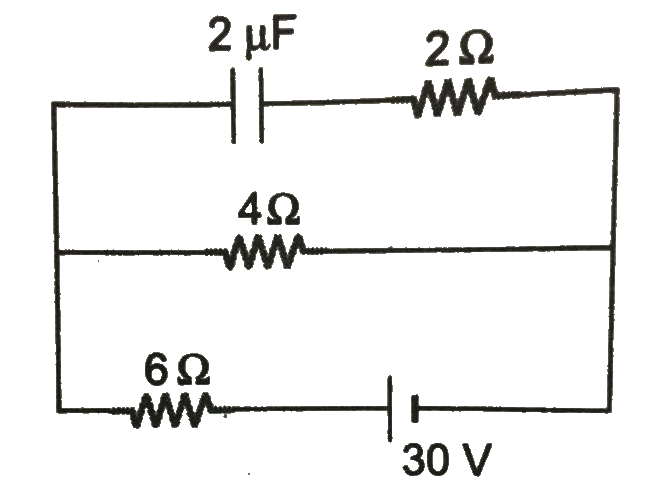
View SolutionFind the charge stored in the capacitor.
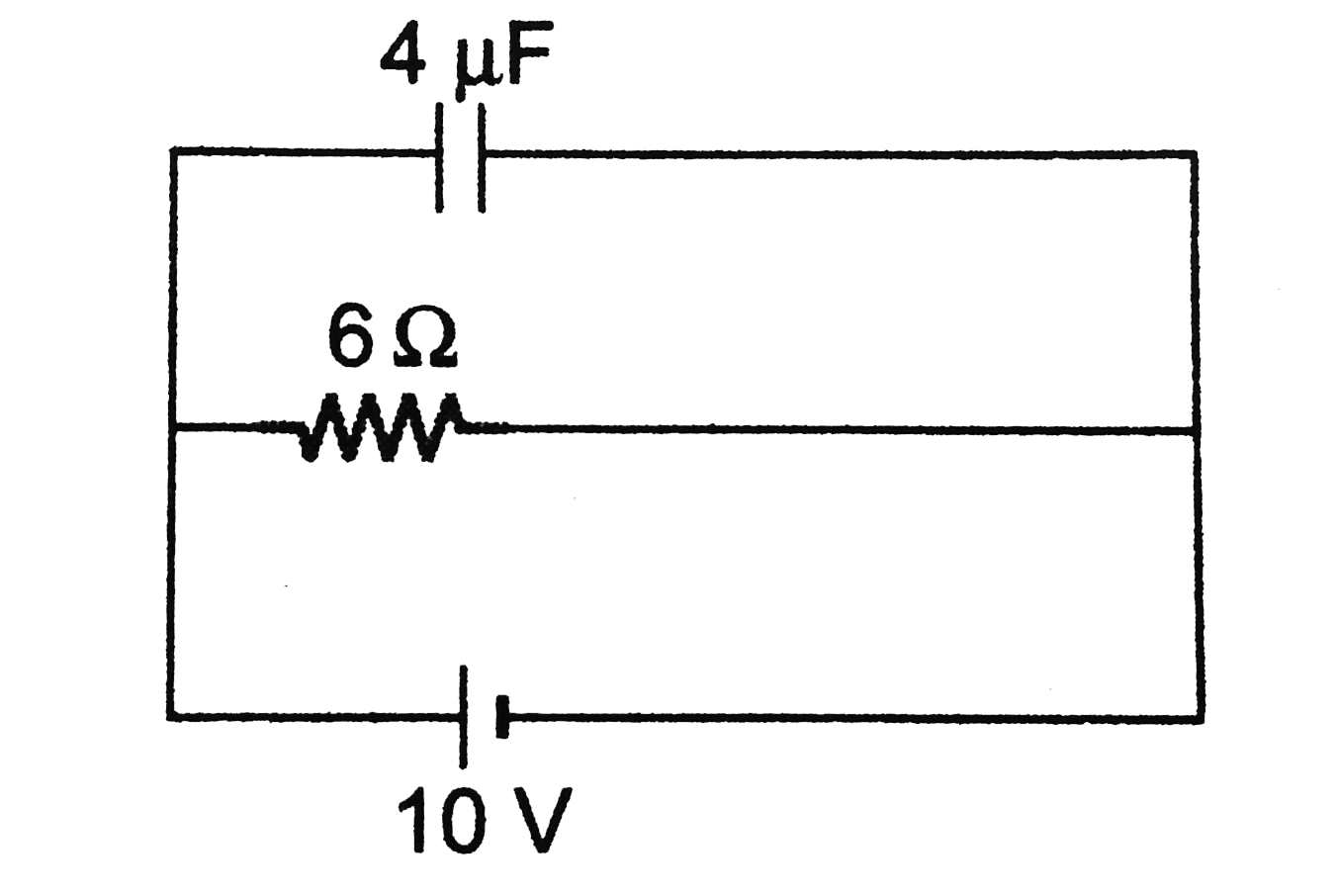
View SolutionFind the charge stored in the capacitor.
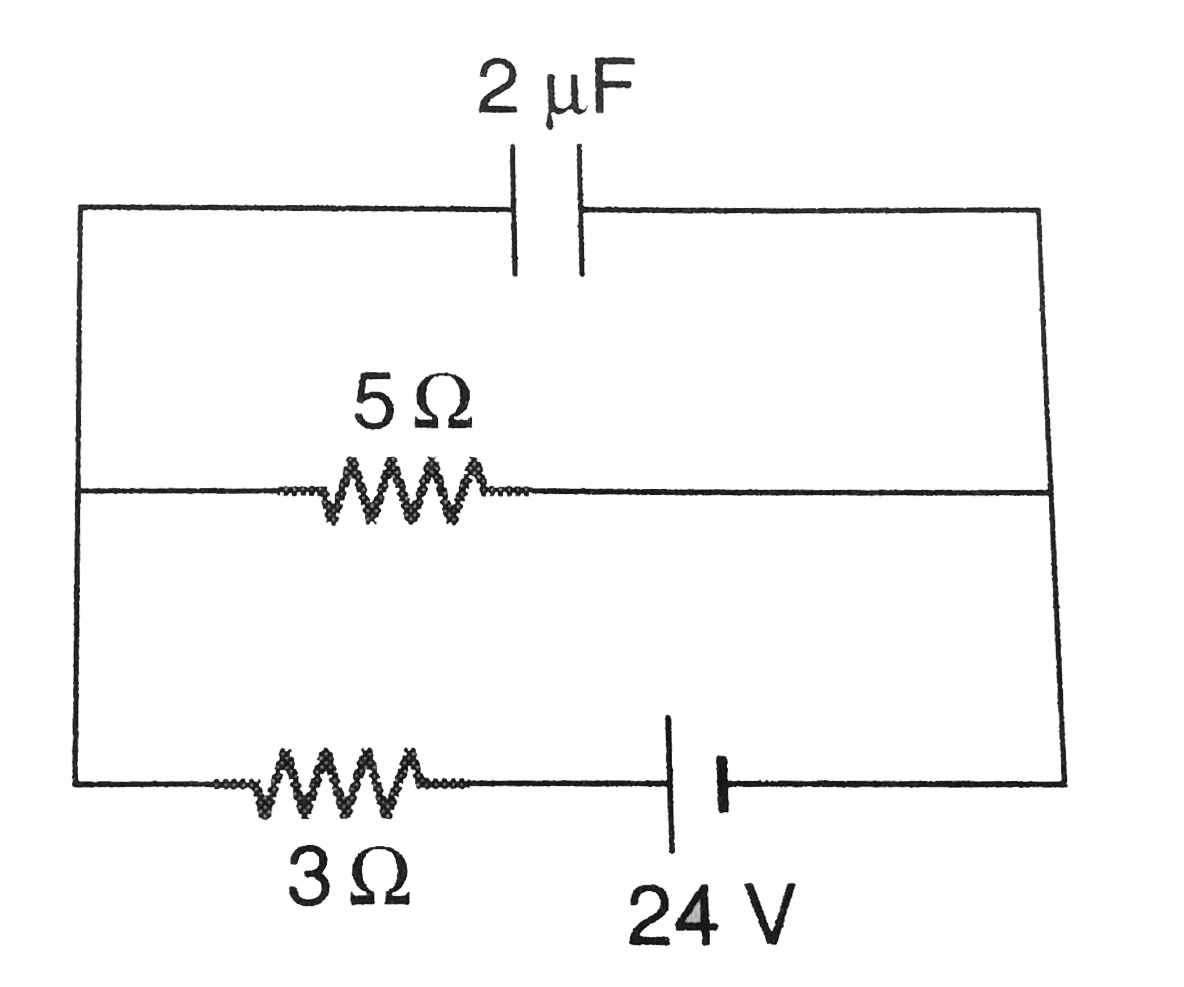
View SolutionFind the total energy stored in the capacitors in the given network.
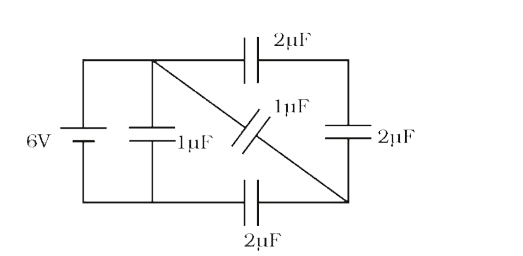
View SolutionFind the charged stored in all the capacitors
View SolutionMatch the columns

View SolutionFind total energy stored in capacitors given in the circuit
View SolutionThe total electrostatic energy stored in both the capacitor is
View Solution

