A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
The correct Answer is:A, B
To find the difference between the pressure of the water in the capillary tube 5.0 cm below the surface and the atmospheric pressure, we can follow these steps:
Step 1: Understand the Problem
We have a capillary tube with a radius of 0.50 mm dipped in water. We need to find the pressure difference between the water in the tube at a depth of 5.0 cm and the atmospheric pressure.
Step 2: Convert Units
Convert the radius of the capillary tube from millimeters to meters:
- Radius r=0.50mm=0.50×10−3m=0.0005m
Step 3: Calculate the Capillary Rise
The formula for capillary rise h is given by:
h=2scosθρgr
Where:
- s = surface tension of water = 0.075 N/m
- θ = contact angle (for water in glass, θ=0∘, so cos0=1)
- ρ = density of water = 1000 kg/m³
- g = acceleration due to gravity = 9.8 m/s²
Substituting the values into the formula:
h=2×0.075×11000×9.8×0.0005
Calculating this gives:
h=0.150.0049≈30.61m
This indicates the height to which water rises in the capillary tube due to surface tension.
Step 4: Calculate the Pressure at 5 cm Depth
The pressure at a depth h in a fluid is given by:
P=ρgh
Where h=5cm=0.05m. Thus:
P=1000×9.8×0.05
Calculating this gives:
P=490N/m2
Step 5: Calculate the Pressure Difference
The pressure difference between the water in the tube at 5 cm depth and the atmospheric pressure (which is the pressure at the surface of the water in the tube) is given by:
ΔP=Pdepth−Patmospheric
Where Patmospheric is equal to the pressure due to capillary rise, which we calculated to be approximately 300N/m2.
Thus:
ΔP=490−300=190N/m2
Final Answer
The difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure is:
ΔP=190N/m2
---
We have a capillary tube with a radius of 0.50 mm dipped in water. We need to find the pressure difference between the water in the tube at a depth of 5.0 cm and the atmospheric pressure.
Convert the radius of the capillary tube from millimeters to meters:
- Radius r=0.50mm=0.50×10−3m=0.0005m
The formula for capillary rise h is given by:
h=2scosθρgr
Where:
- s = surface tension of water = 0.075 N/m
- θ = contact angle (for water in glass, θ=0∘, so cos0=1)
- ρ = density of water = 1000 kg/m³
- g = acceleration due to gravity = 9.8 m/s²
h=2×0.075×11000×9.8×0.0005
Calculating this gives:
h=0.150.0049≈30.61m
This indicates the height to which water rises in the capillary tube due to surface tension.
The pressure at a depth h in a fluid is given by:
P=ρgh
Where h=5cm=0.05m. Thus:
P=1000×9.8×0.05
Calculating this gives:
P=490N/m2
The pressure difference between the water in the tube at 5 cm depth and the atmospheric pressure (which is the pressure at the surface of the water in the tube) is given by:
ΔP=Pdepth−Patmospheric
Where Patmospheric is equal to the pressure due to capillary rise, which we calculated to be approximately 300N/m2.
ΔP=490−300=190N/m2
The difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure is:
ΔP=190N/m2
Topper's Solved these Questions
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Question For short Anser
18 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-1
29 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Worked out Example
17 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SOUND WAVESBOOK - HC VERMA ENGLISHCHAPTER - SOUND WAVESEXERCISE - All Questions
133 Videos
Similar Questions
If the lower end of a capillary tube of radius 2.5 mm is dipped 8 cm below the surface of water in a beaker, then calculate the pressure within a bubble blown at its end in water, in excess of atompheric pressure. [Surface tension of water 72×10−3 N/m]
View SolutionWater is kept in a beaker of radius 5.0 cm. Consider a diameter of the beaker on the surface of the water. Find the force by which the surface on one side of the diameter pulls the surface on the other side. Surface tension of water =0.075Nm−1.
View SolutionA capillary tube of radius 0.20 mm is dipped vertically in water. Find the height of the water column raised in the tube. Surface tension of water =0.075Nm−1 and density of water =1000kgm−3.Takeg=10ms−2.
View SolutionA 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water =0.076Nm−1
View SolutionA uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
View SolutionA capillary tube of inside diameter 1mm is dipped vertically into water, so that the length of its part protruding over the water surface is 20mm.What is the radius of curvatur of the meniscus ? Surface tension of water is 72×10−3N/m.
View SolutionTwo large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm. Find the rise of water in the space between the plates. Surface tension of water =0.075Nm−1.
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
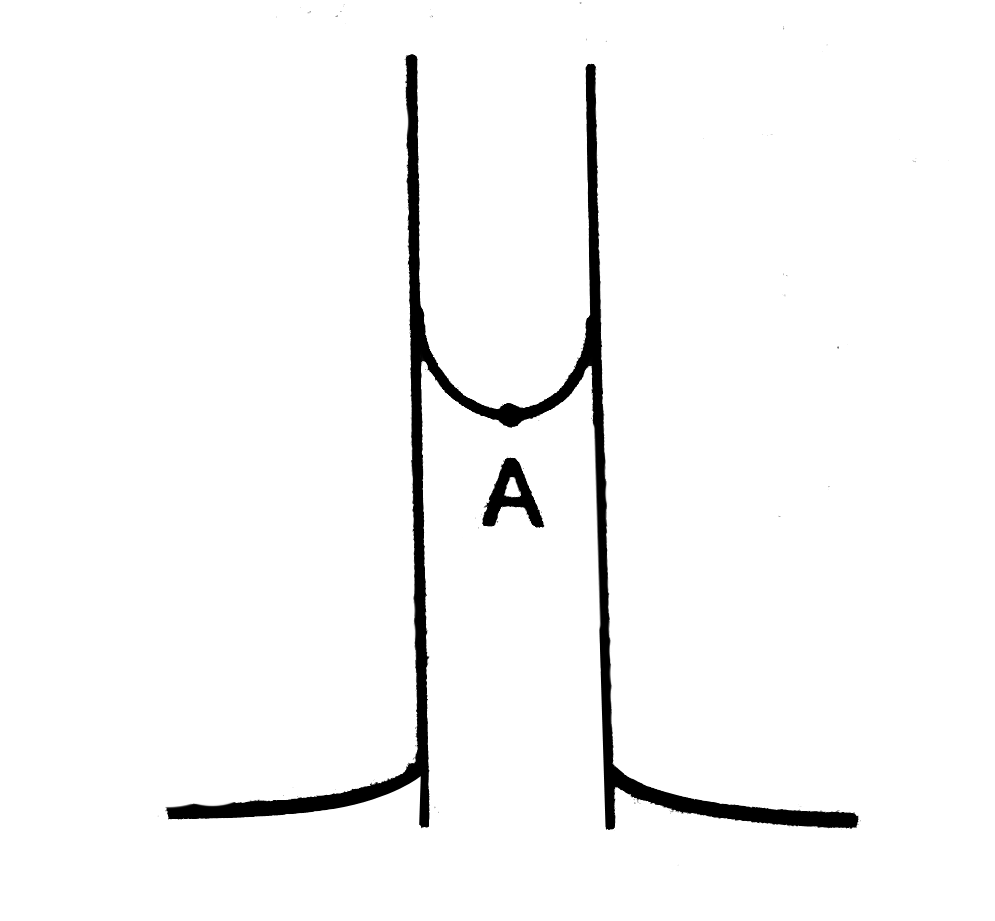
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionA glass capillary tube of internal radius r=0.25mm is immersed in water. The top end of the tube projects by 2cm above the surface of water. At what angle does the liquid meet the tube? Surface tension of water =0.7Nm−1.
View Solution
