A car accelerates from rest at a constant rate α for some time after which it decelerates at a constant rate β to come to rest. If the total time lapse is t seconds , evauate.
(i) maximum velocity reached , and
(ii) the total distance travelled .
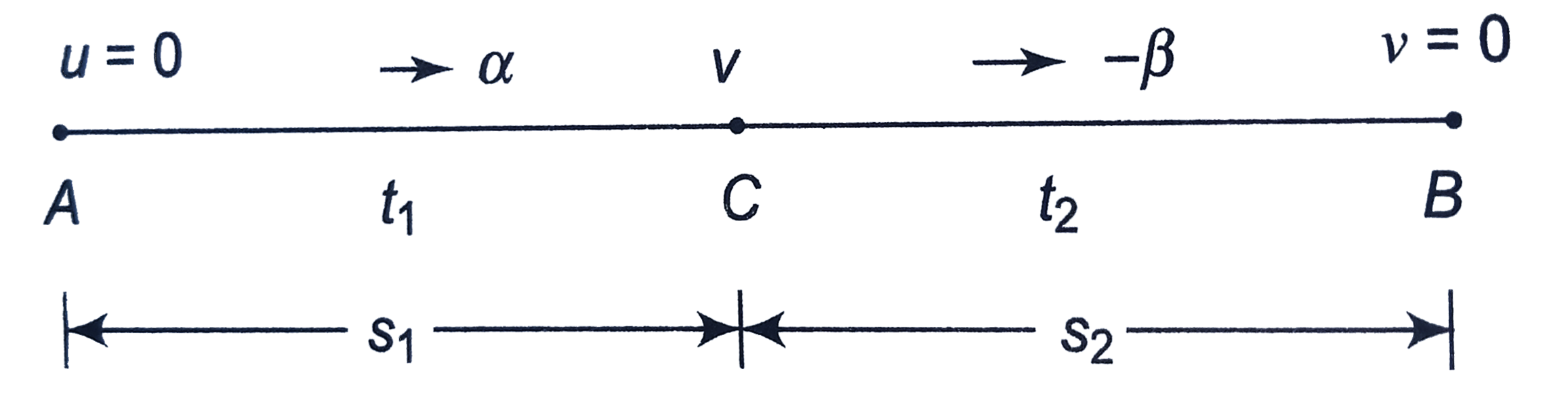
Let the maximum velocity be v.
A to C: (constant acceleration)
v=0+αt1…(i)
v2=0+2αs1…(ii)
C to B: (constant retardation)
0=v−βt2…(iii)
0=v2−2βs2…(iv)
From (i), t1=vα, from (ii), t2=vβ
t1+t2=t(given)
vα+vβ=t
v=αβtα+β
from (i), s1=v22d, from (ii), s2=v22β
Total distance s=s1+s2=v22(1α+1β)
=12(αβtα+β)2(α+βαβ)
=αβt22(α+β)
Topper's Solved these Questions
Similar Questions
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View Solution
Knowledge Check
- Question 1 - Select One
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b) - Question 2 - Select One
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aαβα+βtBα+βαβtCα2+β2βαDα+β2βα - Question 3 - Select One
A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβ
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View Solution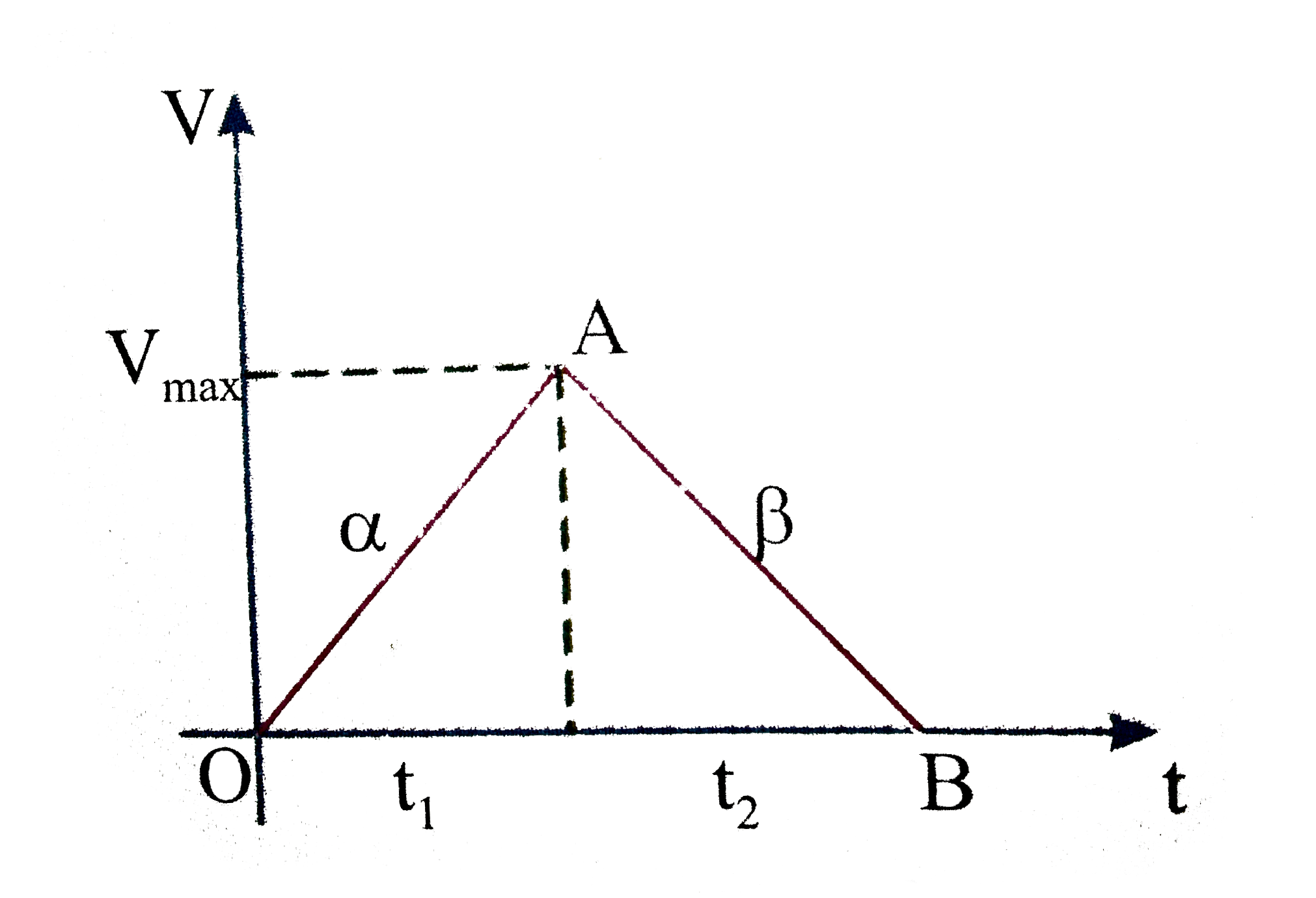
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.View SolutionA car accelerates from rest at acionstant rate 36kmh∘ to comet to rest. If the total time elapsed id 1 hour, calculate (i) the maximum velocity attained by the car and (ii) the total distance travelled by car.
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View Solution

