A car accelerates from rest at a constant rate α for some time t, after which it retards at a constant rate β to come to rest. The total time taken for the trip is t. Find the maximum velocity reached and the total distance convered graphically.
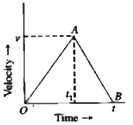
The velocity time graph of the car is as shown in Fig. Let the final maximum velcoity acquired by the car at the end of time t1 be v.
Slope of the line OA = acceleration =α=vt1,t1=vα ……….(i)
Slope of the line AB = retardation =β=vt−t1,t−t1=vβ ...........(ii)
Adding equations (i) and (ii)
t−t1+t1=vα+vβ=v[1α+1β]=v[α+βαβ]
v=[αβα+β]t
Distance travelled by the car = Area of the triangle OAB
=12t×v=12[αβα+β]t2.
Topper's Solved these Questions
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS
20 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS
93 Videos
- DYNAMICSBOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS
12 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
- FRICTIONBOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems
30 Videos
Similar Questions
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute the maximum velocity aquired by the car is
View SolutionA car accelerates from rest at a constant rate 'alpha' for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
View Solution
Knowledge Check
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b)A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβ
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA bus accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds then, evaluate.
(a)the maximum velocity achieved and (b)the total distance travelled graphically.
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View Solution
