A car is moving on a straight road. After covering a distance of 420 m in 18s, it turns back and stops after 8s half the way. Calculate the average velocity of the car in first 20s.
To solve the problem, we will calculate the average velocity of the car over the first 20 seconds of its motion. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the displacement during the first 18 seconds
The car covers a distance of 420 meters in the first 18 seconds. Since it is moving in a straight line, the displacement is also 420 meters.
Displacement after 18 seconds = 420 m
Step 2: Determine the motion after 18 seconds
After 18 seconds, the car turns back. It stops after 8 seconds, covering half the distance it had previously traveled while turning back.
The distance covered while turning back is:
- Half of 420 m = 210 m
Step 3: Calculate the time taken to cover the distance while turning back
The car takes 8 seconds to cover this distance of 210 meters while turning back.
Step 4: Calculate the distance covered in the first 2 seconds of the return journey
Since the car takes 8 seconds to cover 210 meters, we can find the speed during the return journey:
- Speed = Distance / Time = 210 m / 8 s = 26.25 m/s
Now, we need to calculate how far the car travels in the first 2 seconds of the return journey:
- Distance in 2 seconds = Speed × Time = 26.25 m/s × 2 s = 52.5 m
Step 5: Determine the direction of the distance covered during the return journey
Since the car is returning to its starting point, this distance is in the opposite direction to the initial motion. Therefore, we will consider this distance as negative:
- Distance covered while returning in 2 seconds = -52.5 m
Step 6: Calculate the total displacement after 20 seconds
Now, we can calculate the total displacement after 20 seconds:
- Total displacement = Displacement after 18 seconds + Distance covered in the first 2 seconds of return
- Total displacement = 420 m - 52.5 m = 367.5 m
Step 7: Calculate the average velocity
The average velocity is given by the formula:
Average Velocity=Total DisplacementTotal Time
Substituting the values we have:
- Total displacement = 367.5 m
- Total time = 20 s
So,
Average Velocity=367.5m20s=18.375m/s
Final Answer
The average velocity of the car in the first 20 seconds is approximately 18.38 m/s.
---
The car covers a distance of 420 meters in the first 18 seconds. Since it is moving in a straight line, the displacement is also 420 meters.
After 18 seconds, the car turns back. It stops after 8 seconds, covering half the distance it had previously traveled while turning back.
- Half of 420 m = 210 m
The car takes 8 seconds to cover this distance of 210 meters while turning back.
Since the car takes 8 seconds to cover 210 meters, we can find the speed during the return journey:
- Speed = Distance / Time = 210 m / 8 s = 26.25 m/s
- Distance in 2 seconds = Speed × Time = 26.25 m/s × 2 s = 52.5 m
Since the car is returning to its starting point, this distance is in the opposite direction to the initial motion. Therefore, we will consider this distance as negative:
- Distance covered while returning in 2 seconds = -52.5 m
Now, we can calculate the total displacement after 20 seconds:
- Total displacement = Displacement after 18 seconds + Distance covered in the first 2 seconds of return
- Total displacement = 420 m - 52.5 m = 367.5 m
The average velocity is given by the formula:
Average Velocity=Total DisplacementTotal Time
- Total displacement = 367.5 m
- Total time = 20 s
Average Velocity=367.5m20s=18.375m/s
The average velocity of the car in the first 20 seconds is approximately 18.38 m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - COMPETITION FILE (INTEGER TYPE QUESTIONS )
9 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
A bike is moving on a straight road After covering a distance of 420m in 22 sec, it turns back and stops after 12sec midway. Calculate the average velocity of the bike in first 22 sec and in first 34sec.
View SolutionA car covers a distance of 108.9 km in 1.8 hours. What is the average speed of the car?
View Solution
Knowledge Check
A car is moving on a straight road covers one third of the distance with a speed of 20 km/h and the rest with a speed of 60 km/h. The average speed of the car is
A40 km/hB50 km/hC36 km/hD55 km/hA car travels half the distance with a constant velocity of 40m/s and the remaining half with a constant velocity of 60m/s. The average velocity of the car in m/s is
A42B50C48D45The velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car in first 25 seconds is
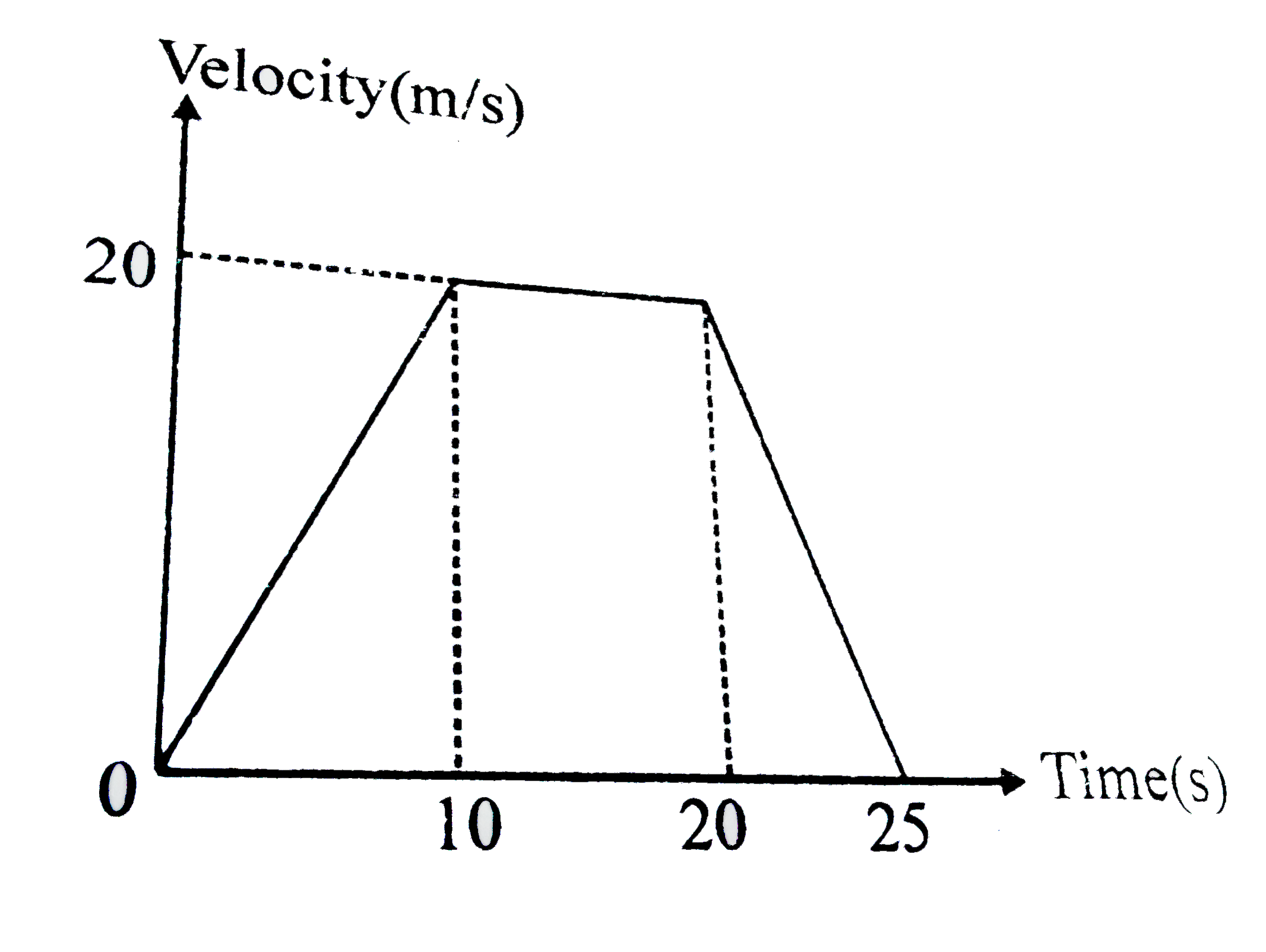 A20m/sB14m/sC10m/sD17.5m/s
A20m/sB14m/sC10m/sD17.5m/s
A scooter is moving along a straight line AB covers a distance of 360 m in 24 s and returns back from B to C and coveres 240 m in 18 s. Find the total distance travelled by the scooter.
View SolutionA car is moving along a straight (OP). It moves from O→P in 18seconds amd retuns from P→Q in 6 seconds,whereOP=360 mandOQ=240 m What are the car the average velcoty and average speed of the car in going (a) from O→P and back to Q ?
View SolutionA boy swims in a 100 m long pool. He covers 60 m with a velocity of 20 m/s and covers the rest of the distance with a velocity of 10 m/s. Calculate the average velocity of the boy.
View SolutionA car is travelling along a straight line and covers one-fourth of the total distance with a velocity of 10m/s. the remaining distance is covered with a velocity of 5m/s. calculate the average velocity of the car.
View SolutionA car is moving along a straight (OP). It moves from OtoP in 18seconds and returns from PtoQ in 6 seconds, where OP=360m and OQ=240m What are the car the average velocity and average speed of the car in going (a) from OtoP and back to Q?
View Solution
