A car is moving with a speed of 10ms−1, If the east direction taken as x-axis and the north direction as y-axis . Write the velocity vector of car in unit vector notation.If it is moving (a) in the direction of N-E,(b) in the direction of N−W,(C ) in the direction ofS−W, and (d) in the direction of S−E.
To solve the problem of determining the velocity vector of a car moving at a speed of 10m/s in various directions, we will express the velocity vector in unit vector notation for each specified direction. The east direction is taken as the x-axis and the north direction as the y-axis.
1. Understanding Unit Vector Notation:
- The velocity vector can be expressed in the form →v=vx^i+vy^j, where vx is the component in the x-direction (east) and vy is the component in the y-direction (north).
2. Magnitude of Velocity:
- The car is moving with a speed of 10m/s.
3. Direction: North-East (NE):
- The angle with respect to the x-axis (east) is 45∘.
- The components can be calculated as:
vx=10cos(45∘)=10⋅1√2=10√2≈7.07m/s
vy=10sin(45∘)=10⋅1√2=10√2≈7.07m/s
- Therefore, the velocity vector is:
→vNE=10√2^i+10√2^j≈7.07^i+7.07^j
4. Direction: North-West (NW):
- The angle with respect to the x-axis (east) is 135∘.
- The components can be calculated as:
vx=10cos(135∘)=10⋅(−1√2)=−10√2≈−7.07m/s
vy=10sin(135∘)=10⋅1√2=10√2≈7.07m/s
- Therefore, the velocity vector is:
→vNW=−10√2^i+10√2^j≈−7.07^i+7.07^j
5. Direction: South-West (SW):
- The angle with respect to the x-axis (east) is 225∘.
- The components can be calculated as:
vx=10cos(225∘)=10⋅(−1√2)=−10√2≈−7.07m/s
vy=10sin(225∘)=10⋅(−1√2)=−10√2≈−7.07m/s
- Therefore, the velocity vector is:
→vSW=−10√2^i−10√2^j≈−7.07^i−7.07^j
6. Direction: South-East (SE):
- The angle with respect to the x-axis (east) is 315∘.
- The components can be calculated as:
vx=10cos(315∘)=10⋅1√2=10√2≈7.07m/s
vy=10sin(315∘)=10⋅(−1√2)=−10√2≈−7.07m/s
- Therefore, the velocity vector is:
→vSE=10√2^i−10√2^j≈7.07^i−7.07^j
Summary of Velocity Vectors:
- North-East: →vNE=7.07^i+7.07^j
- North-West: →vNW=−7.07^i+7.07^j
- South-West: →vSW=−7.07^i−7.07^j
- South-East: →vSE=7.07^i−7.07^j
- The velocity vector can be expressed in the form →v=vx^i+vy^j, where vx is the component in the x-direction (east) and vy is the component in the y-direction (north).
- The car is moving with a speed of 10m/s.
- The angle with respect to the x-axis (east) is 45∘.
- The components can be calculated as:
vx=10cos(45∘)=10⋅1√2=10√2≈7.07m/s
vy=10sin(45∘)=10⋅1√2=10√2≈7.07m/s
- Therefore, the velocity vector is:
→vNE=10√2^i+10√2^j≈7.07^i+7.07^j
- The angle with respect to the x-axis (east) is 135∘.
- The components can be calculated as:
vx=10cos(135∘)=10⋅(−1√2)=−10√2≈−7.07m/s
vy=10sin(135∘)=10⋅1√2=10√2≈7.07m/s
- Therefore, the velocity vector is:
→vNW=−10√2^i+10√2^j≈−7.07^i+7.07^j
- The angle with respect to the x-axis (east) is 225∘.
- The components can be calculated as:
vx=10cos(225∘)=10⋅(−1√2)=−10√2≈−7.07m/s
vy=10sin(225∘)=10⋅(−1√2)=−10√2≈−7.07m/s
- Therefore, the velocity vector is:
→vSW=−10√2^i−10√2^j≈−7.07^i−7.07^j
- The angle with respect to the x-axis (east) is 315∘.
- The components can be calculated as:
vx=10cos(315∘)=10⋅1√2=10√2≈7.07m/s
vy=10sin(315∘)=10⋅(−1√2)=−10√2≈−7.07m/s
- Therefore, the velocity vector is:
→vSE=10√2^i−10√2^j≈7.07^i−7.07^j
- North-East: →vNE=7.07^i+7.07^j
- North-West: →vNW=−7.07^i+7.07^j
- South-West: →vSW=−7.07^i−7.07^j
- South-East: →vSE=7.07^i−7.07^j
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.1
19 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
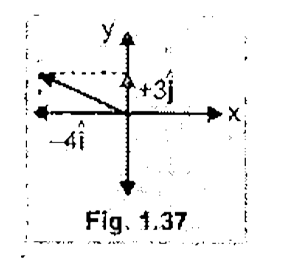
A car is moving in direction →r=−4ˆi+3ˆj with a speed of 10ms−1. Write the velocity vector of car in unit vector notation.
View SolutionA boat is moving in direction −4ˆi+3ˆj with ,a speed of 10 rn/s. Write velocity vector of boat in unit vector notation. Direction of motion of boat is along unit vector :
View Solution
Knowledge Check
A car is moving in east direction. It takes a right turn and moves along south direction without change in its speed. What is the direction of average acceleration of the car?
ANorth eastBSouth eastCNorth westDSouth westA car moves with speed 60km/h for 1 hour in east direction and with same speed for 30 min in south direction. The displacement of car from initial posilion is
A60 kmB30√3kmC30√5kmD60√2kmA car is moving with velocity →vc towards north and a train is moving towards east with velocity →vt . Find the direction of relative velocity of car with respect to train.
AWestBNorthCN-WDS-W
A bird moves with velocity 20ms−1 in a direction making an angle of 60∘ with vertical upward .Represent the velocity vector in a rectangular form.
View SolutionThe position vector →r of a particle points along the positive direction of a z axis. If the torque on the particle is (a) zero, (b) in the negative direction of x, and ( c) in the negative direction of y, in what direction is the force causing the torque?
View SolutionA particle is moving with speed 6m/s along the direction of 2ˆi+2ˆj−ˆk find the velocity vector of a particle ?
View SolutionA and B are moving with the same speed 10m/s in the direction E−30∘−N and E−30∘−S respectively. Find the relative velocity of A w.r.t. B.
View SolutionA vector has a component of 15 m in the + x direction, a component of 15 m in the + y direction, and a component of 1- m in the + z direction. What is the magnitude of this vector ?
View Solution
