A car of mass m has an engine which can deliver power P. The minimum time in which car can be accelerated from rest to a speed v is :-
Pmv2
mv22P
2Pmv2
mv2P
The correct Answer is:B
Power = Force × Velocity
In this case, the required force
= weight of the lift + frictional force =mg+F
=1800×10+4000=22000N
∴ Power =Fv=22000×2=44000 watt
∴P=44kW
Topper's Solved these Questions
Similar Questions
On a horizontal rought rood , value of coefficient of friction μ=0.4.Find the minimum time in which a distance of 400m can be covered. The car start from rest and finally comes to rest.
View SolutionA railroad flatcar of mass M can roll without friction along a straight horizontal track. Initially, a man of mass 'm' is standing on the car, which is at rest. What is the velocity of the car if man runs to the left so that his speed relative to the car is vrel.
View Solution
Knowledge Check
A car of mass mhasan engine which can deliver constant power P.the maximum speed that the car can attain in t seconds in
A√34PtmB2√PtmC√2PtmD√PtmThe coefficient of friction between a car wheels and a roadway is 0.5 The least distance in which the car can accelerate from rest to a speed of 72 kmph is (g=10ms−2)
A10mB20mC30mD40mA car is travelling on a road. The maximum velocity the car can attain is 24ms−1 and the maximum deceleration is 4ms−2. If car starts from rest and comes to rest after travelling 1032m in the shortest time of 56 s, the maximum acceleration that the car can attain is
A1.2m/s2B3.6m/s2C6m/s2D12m/s2
If the crest of the hill has a radius of curvature p determine the maximum constnat speed at which the car can travel over it without leaving the surface of the road. Neglect the size of the car in the calculation. The car has mass m. Given p=40m, m=1700kg, g=10m/s2
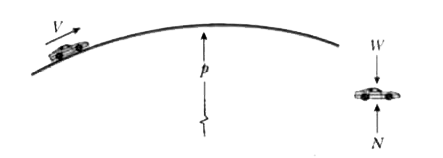
View SolutionThe coefficient of friction between the ground and the wheels of a car between the ground and the wheels of acar moving on a horizontal road is 0.5 If the car starts from rest , what is the minimum distance in which it can acquire a speed of 72km/h ? take g=10ms−2 .
View SolutionA car starts from rest to cover a distance s. the coefficient of friction between the road and the tyres is μ. The minimum time in which the car can cover the distance is proportional to
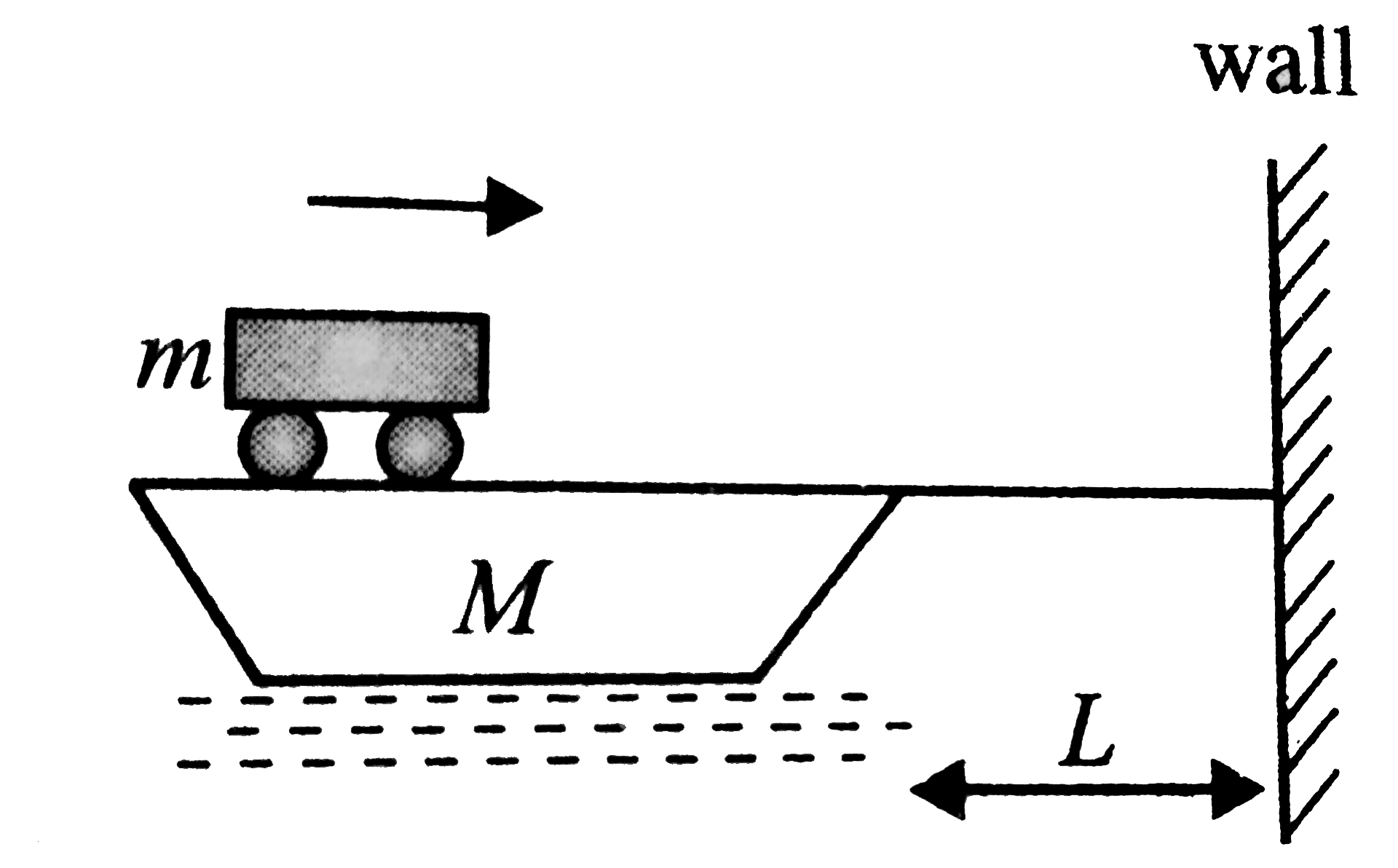
View SolutionA car of mass m is initially at rest on the boat of mass M tied to the wall of dock through a massless, inextensible string. The car accelerates from rest to velocity v0 in times to. At t=t0 the car applies brake and comes to rest relative to the boat in negligible time. Neglect friction between the boat and water: the time 't' at which boat will strike the wall is
View SolutionA car starts from rest. It has to cover a distane of 500m from rest to rest. The coefficient of friction between the road and the tyre is 1/2. the minimum time in which the car can cover this distance is? (g=10m/s2)
View Solution
