A certain species of ionized atoms produces emission line spectral accorduing to the Bohr's model. A group of lines in the spectrum is forming a series in which in the shortest wavelength is 22.79nm and the longest wavelength is 41.02nm. The atomic number of atom is Z.
Based on above information, answer the following question:
The series belongs to
Lyman
Balmer
Paschen
Brackett
The correct Answer is:B
To determine which series the given wavelengths belong to, we can follow these steps:
1. Identify the Given Wavelengths:
- Shortest wavelength (λ_min) = 22.79 nm
- Longest wavelength (λ_max) = 41.02 nm
2. Understand the Energy-Wavelength Relationship:
- The energy (E) of a photon is inversely related to its wavelength (λ) by the equation:
E=hcλ
- Where h is Planck's constant and c is the speed of light.
3. Establish the Energy Conditions:
- The shortest wavelength corresponds to the maximum energy transition (from a higher energy level to n = 1).
- The longest wavelength corresponds to the minimum energy transition (from n = 2 to n = 1).
4. Set Up the Energy Equations:
- For the shortest wavelength (λ_min):
Emin=hcλmin=13.6Z2(112−1n2)
- For the longest wavelength (λ_max):
Emax=hcλmax=13.6Z2(1n2−1(n+1)2)
5. Divide the Two Equations:
- By dividing the two energy equations, we can eliminate constants and solve for n:
λminλmax=1−1n21n2−1(n+1)2
6. Substitute the Values:
- Substitute λ_min = 22.79 nm and λ_max = 41.02 nm into the equation:
22.7941.02=1−1n21n2−1(n+1)2
7. Solve for n:
- After simplifying and solving the equation, we find n≈2.
8. Determine the Series:
- Since the transition ends at n=2, this corresponds to the Balmer series (which involves transitions to the n=2 level).
Conclusion:
The series belongs to the Balmer series.
- Shortest wavelength (λ_min) = 22.79 nm
- Longest wavelength (λ_max) = 41.02 nm
- The energy (E) of a photon is inversely related to its wavelength (λ) by the equation:
E=hcλ
- Where h is Planck's constant and c is the speed of light.
- The shortest wavelength corresponds to the maximum energy transition (from a higher energy level to n = 1).
- The longest wavelength corresponds to the minimum energy transition (from n = 2 to n = 1).
- For the shortest wavelength (λ_min):
Emin=hcλmin=13.6Z2(112−1n2)
- For the longest wavelength (λ_max):
Emax=hcλmax=13.6Z2(1n2−1(n+1)2)
- By dividing the two energy equations, we can eliminate constants and solve for n:
λminλmax=1−1n21n2−1(n+1)2
- Substitute λ_min = 22.79 nm and λ_max = 41.02 nm into the equation:
22.7941.02=1−1n21n2−1(n+1)2
- After simplifying and solving the equation, we find n≈2.
- Since the transition ends at n=2, this corresponds to the Balmer series (which involves transitions to the n=2 level).
The series belongs to the Balmer series.
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Integer
4 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Fill In The Blanks
8 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct
13 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
A certain species of ionized atoms produces emission line spectral accorduing to the Bohr's model. A group of lines in the spectrum is forming a series in which in the shortest wavelength is 22.79nm and the longest wavelength is 41.02nm. The atomic number of atom is Z.
Based on above information, answer the following question:
The next to longest wavelength in the series of lines is
View SolutionA series of linenes in the spectrum of atomic H lies at wavelength 656.46,486.27,434.17,410.29nm What is the wavelength of the line in this series ?
View SolutionAn element Z has atomic number 16. Answer the following questions on Z:
State the period and group to which z belongs.
View SolutionA monochromatic beam of light having photon energy 12.5eV is incident on a simple A of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample B of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The emission spectra of sample A
View SolutionA monochromatic beam of light having photon energy 12.5eV is incident on a simple A of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample B of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The atoms of sample A after passing of light through it
View SolutionA monochromatic beam of light having photon energy 12.5eV is incident on a simple A of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample B of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The atoms of sample B
View SolutionThe shortest wavelength spectral line in the brackett series of the spectrum of atomic hydrogen is the transition :
View SolutionWhich of the following links lines of the H-atom spectrum belongs to the Balmer series ?
View SolutionSimplified model of electron energy levels for a cartain atom is shown in figure. The atom is bombarded will fast moving electrons. The impact of one of these electrons can cause the removal of electron from K-level , thus, creating a vacancy in the K-level. This vacancy in K-level is filled by an electron from l-level and the energy reased in this transition can either appear as electromagnetic waves or may all be used knock out an electron from M-level of the atom.
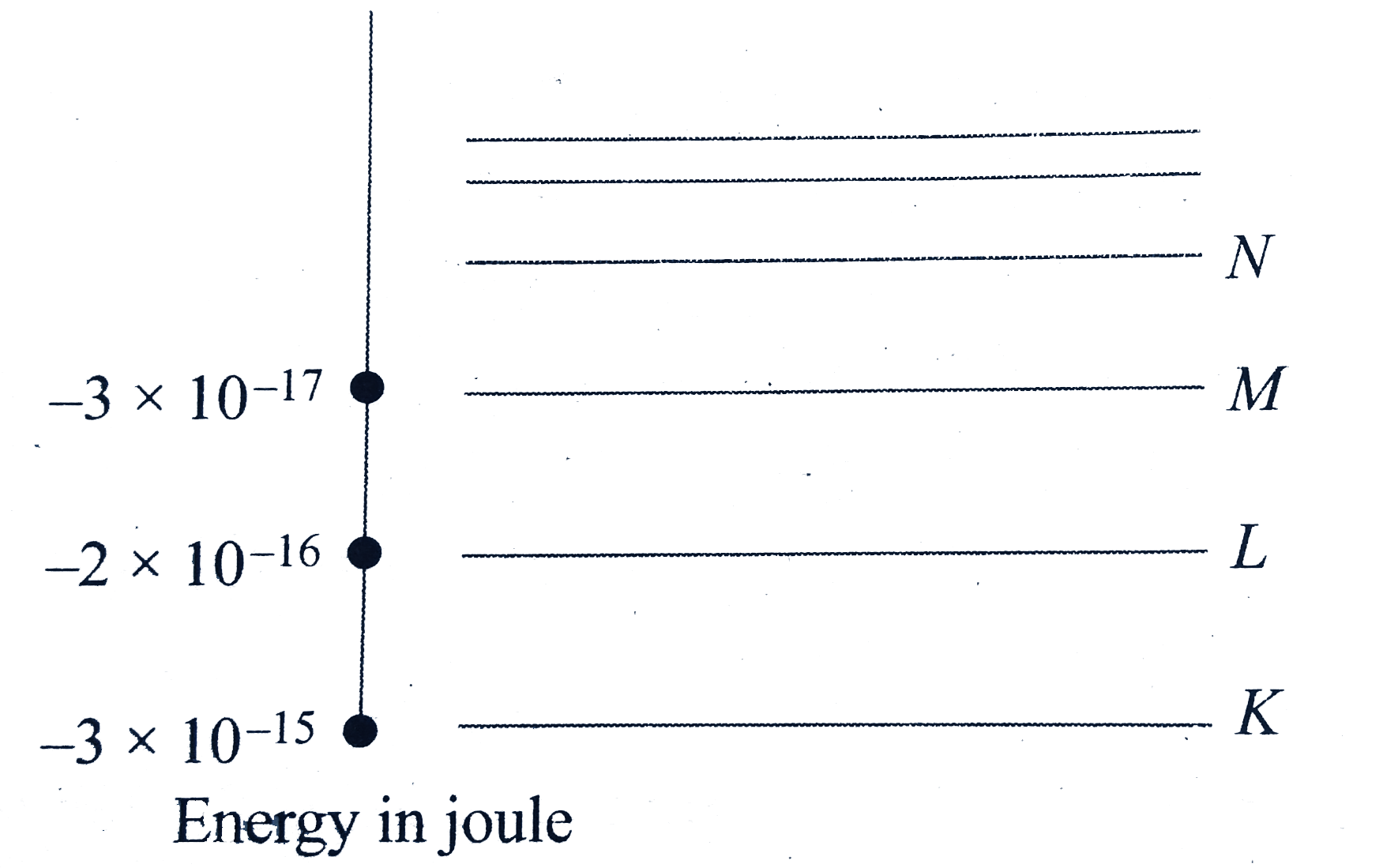
Based on above information, answer the following question:
Wavelength of the electromagnetic waves emitted due to transition from L to K-level is
View SolutionSimplified model of electron energy levels for a cartain atom is shown in figure. The atom is bombarded will fast moving electrons. The impact of one of these electrons can cause the removal of electron from K-level , thus, creating a vacancy in the K-level. This vacancy in K-level is filled by an electron from l-level and the energy reased in this transition can either appear as electromagnetic waves or may all be used knock out an electron from M-level of the atom.
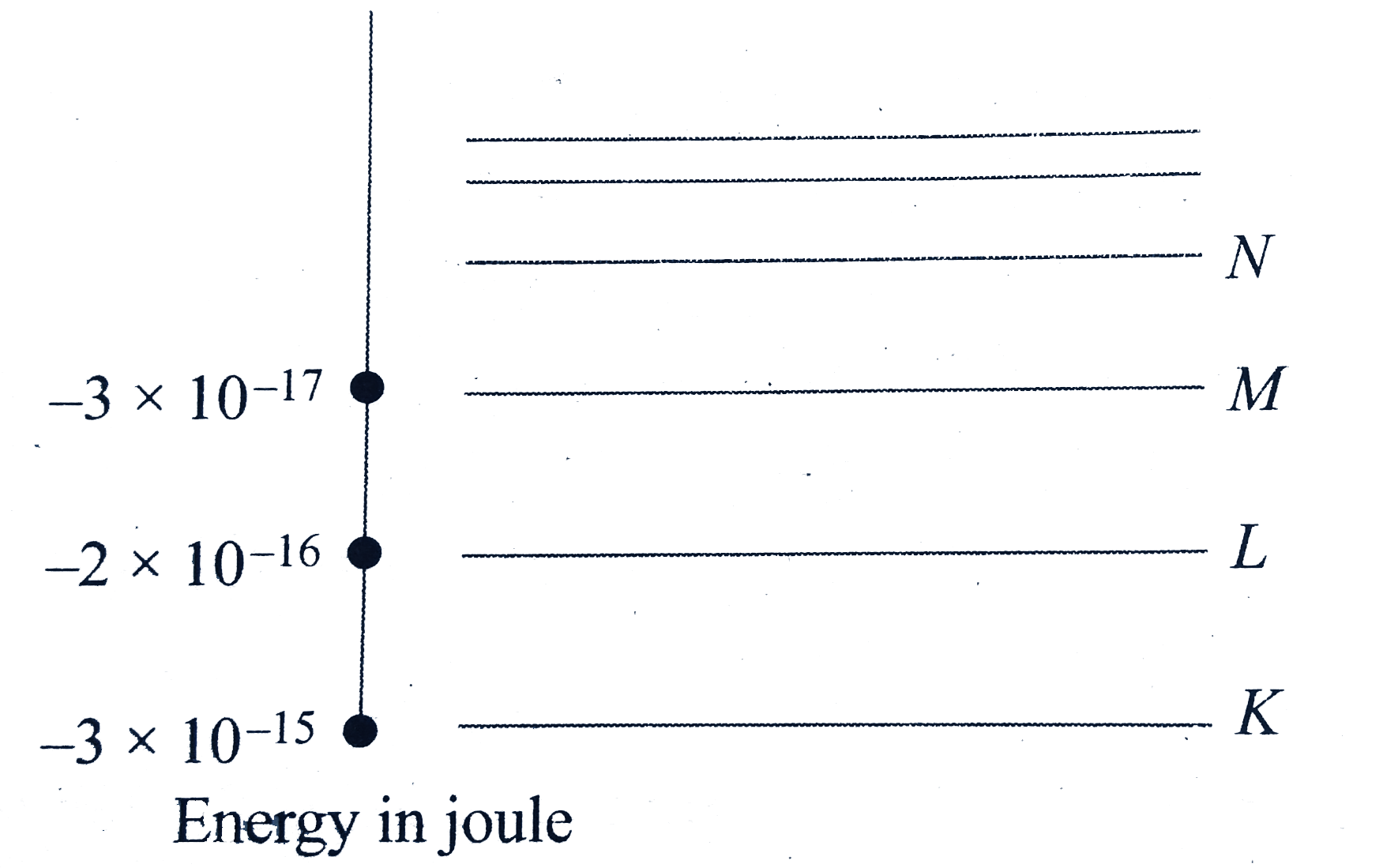
Based on above information, answer the following question:
The minimum potential difference through which bombarding electron beam must be acclerated from rest to cause the ejection of electron from K-level is.
View Solution
